Понятие мультиколленеарности
Мультиколлинеарность – нарушение одного из основных условий, лежащих в основе построения линейной модели множественной регрессии. Мультиколлинеарность может проявляться в функциональной (явной) и стохастической (скрытой) формах. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК). Мультиколлинеарность в матричном виде – это зависимость между столбцами матрицы факторных переменных Х:
Если не учитывать единичный вектор, то размерность данной матрицы равна n*n. Если ранг матрицы Х меньше n, то в модели присутствует полная или строгая мультиколлинеарность. Но на практике полная мультиколлинеарность почти не встречается. Чем сильнее мультиколлинеарность факторных переменных, тем менее надежной является оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов. Включение в модель мультиколлинеарных факторов нежелательно по нескольким причинам: 1) основная гипотеза о незначимости коэффициентов множественной регрессии может подтвердиться, но сама модель регрессии при проверке с помощью F-критерия оказывается значимой, что говорит о завышенной величине коэффициента множественной корреляции; 2) полученные оценки коэффициентов модели множественной регрессии могут быть неоправданно завышены или иметь неправильные знаки; 3) добавление или исключение из исходных данных одного-двух наблюдений оказывает сильное влияние на оценки коэффициентов модели; 4) мультиколлинеарные факторы, включённые в модель множественной регрессии, способны сделать её непригодной для дальнейшего применения. Причинные мультиколлинеарности: 1. Ошибочное включение в уравнение двух и более линейно независимых переменных 2. Две или более объясняющие переменные, в нормальной ситуации слабо коррелированные, становятся в конкретных условиях выборки сильно коррелированными; 3. В модель включается переменная, сильно коррелирующая с зависимой переменной (такая независимая переменная называется доминантой). 5. Методы обнаружения мультиколлинеарности Корреляционной матрицей факторных переменных называется симметричная относительно главной диагонали матрица линейных коэффициентов парной корреляции факторных переменных:
где rij – линейный коэффициент парной корреляции между i -м и j -ым факторными переменными, При рассмотрении данной матрицы с целью выявления мультиколлинеарных факторов руководствуются следующими правилами: 1) если в корреляционной матрице факторных переменных присутствуют коэффициенты парной корреляции по абсолютной величине большие 0,8, то делают вывод, что в данной модели множественной регрессии существует мультиколлинеарность; 2) вычисляют собственные числа корреляционной матрицы факторных переменных λmin и λmax. Если λmin‹10-5, то в модели регрессии присутствует мультиколлинеарность. Если отношение 3) вычисляют определитель корреляционной матрицы факторных переменных. Если его величина очень мала, то в модели регрессии присутствует мультиколлинеарность.
|


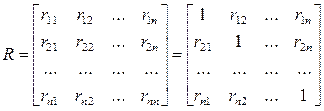 ,
,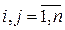 .
.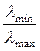 < 10 -5,то также делают вывод о наличии мультиколлинеарных факторных переменных;
< 10 -5,то также делают вывод о наличии мультиколлинеарных факторных переменных;


