Понятия устойчивой и неустойчивой цепи.
Цепь называется устойчивой, если свободные колебания с течением времени стремятся к нулю. В противном случае цепь называется неустойчивой. Из теории переходных процессов следует, что цепь является устойчивой, если корни характеристического уравнения лежат в левой полуплоскости комплексной переменной р. Если корни такого уравнения лежат в правой полуплоскости, то цепь является неустойчивой, т. е. она находится в режиме самовозбуждения. Таким образом, для определения условий устойчивости цепи достаточно найти характеристическое уравнение и его корни. Как видим, условия устойчивости можно определить и, не вводя понятие обратной связи. Однако здесь возникает ряд проблем. Дело в том, что вывод характеристического уравнения и определение его корней являются громоздкой процедурой, особенно для цепей высокого порядка. Введение понятия обратной связи облегчает получение характеристического уравнения или даже дает возможность обойтись без него. Крайне важно и то, что понятие обратной связи адекватно физическим процессам, возникающим в цепи, поэтому они становятся более наглядными. Глубокое понимание физических процессов облегчает работу по созданию автогенераторов, усилителей.
2. Для приведенной структурной схемы представить передаточную функцию. Описать процесс получения результата.
Структурная схема САУ в простейшем случае строится из элементарных динамических звеньев. Но несколько элементарных звеньев могут быть заменены одним звеном со сложной передаточной функцией. Для этого существуют правила эквивалентного преобразования структурных схем. Рассмотрим возможные способы преобразований: 1. Последовательное соединение (рис.2) - выходная величина предшествующего звена подается на вход последующего.

y0 y1 y2 yn
(Рис. 2) То есть цепочка последовательно соединенных звеньев преобразуется в эквивалентное звено с передаточной функцией, равной произведению передаточных функций отдельных звеньев. 2. Параллельно - согласное соединение (рис.3) - на вход каждого звена подается один и тот же сигнал, а выходные сигналы складываются. Тогда:
y1
. . yn y
(Рис.3) То есть цепочка звеньев, соединенных параллельно - согласно, преобразуется в звено с передаточной функцией, равной сумме передаточных функций отдельных звеньев. 3. Параллельно - встречное соединение (рис. 4) - звено охвачено положительной или отрицательной обратной связью. Участок цепи, по которому сигнал идет в противоположном направлении по отношению к системе в целом (то есть с выхода на вход) называется цепью обратной связи с передаточной функцией W ос.
- для положительной ОС.
Для заданной схемы:
1) W2(p) + W3(p) = (Преобразование параллельных элементов)
2). W1(p) * (W2(p) +W3(p)) =
= (Преобразование последовательных элементов)
3). Wэкв.=
3. Для приведенной электрической принципиальной схемы выполните следующие действия: - Составить дифференциальное уравнение электрической цепи - Определить переходную функцию и построить ее график - Определить передаточную функцию, используя преобразование Лапласа - Определить и построить амплитудную частотную характеристику цепи - Определить и построить фазовую частотную характеристику цепи - Сделать вывод об устойчивости схемы
1. Составить дифференциальное уравнение электрической цепи: На основании второго закона Кирхгофа при нулевых начальных условиях составим уравнение:
Выходное напряжение:
Откуда определим значение тока:
Подставим (3) в (1):
Уравнение (4) приводится к стандартной форме:
В операторной форме уравнение (5) представляется как
|

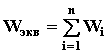 y0 y2
y0 y2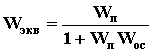 - для отрицательной ОС:
- для отрицательной ОС: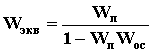
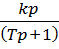 +
+  =
= 
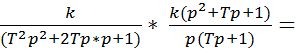
 =
= 
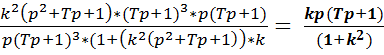
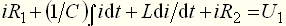 . (1)
. (1)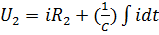 (2)
(2)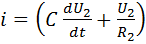 (3)
(3) (4)
(4)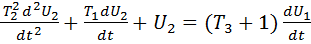 (5), где
(5), где .
.



