Связь показателей Ляпунова с типами аттракторов
Обычно показатели Ляпунова располагают в порядке убывания. Например, символы (+, 0, -) означают, что у некоторого аттрактора в трёхмерном пространстве состояний вдоль одного направления происходит экспоненциальное растяжение, вдоль другого фазовый поток обладает нейтральной устойчивостью и вдоль третьего направления траектории претерпевают экспоненциальное сжатие. Важно отметить, что у аттракторов, отличных от устойчивых стационарных точек, всегда имеется по крайней мере один показатель Ляпунова, равный нулю, так как в среднем точки на траектории ограничены компактным множеством и не могут ни расходиться особенно далеко, ни скапливаться.
1) n = 1.
2) n = 2.
3) n = 3.
Т.о., в системе со странным аттрактором (+, 0, -) вдоль одного направления происходит экспоненциальное расхождение траекторий, вдоль другого – наблюдается нейтральная устойчивость и вдоль третьего – траектории экспоненциально стягиваются. Причём, сумма показателей Ляпунова для системы, имеющей аттрактор, всегда должна быть отрицательна. Например, для системы Лоренца показатели Ляпунова имеют значения:
Пример Рассмотрим двумерную систему:
Зададим для неё начальное состояние:
Выберем другое начальное состояние с учётом смещения по х 1:
Построим от этих начальных состояний траектории и определим расстояние d между соответствующими точками этих траекторий:
В начальный момент времени это расстояние будет равно:
Показатель Ляпунова будет определяться по формуле:
Аналогично задаём исходное смещение по х 2 и определяем другой показатель Ляпунова:
Рассмотрим конкретный пример:
Зададим начальное состояние:
Решаем систему:
Находим константы интегрирования:
Выберем другое начальное состояние с учётом смещения по х 1:
Построим от этих начальных состояний траектории и определим расстояние d между соответствующими точками этих траекторий:
Определим показатель Ляпунова:
Зададим исходное смещение по х 2 и определим другой показатель Ляпунова:
Т.о., данная система имеет устойчивую неподвижную точку.
Аналитическое определение показателей Ляпунова для большинства задач невозможно, поскольку для этого необходимо знать аналитическое решение системы дифференциальных уравнений. Поэтому, как правило, для определения показателей Ляпунова используют численные методы.
|

 – устойчивая неподвижная точка – аттрактор,
– устойчивая неподвижная точка – аттрактор,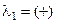 – неустойчивая неподвижная точка.
– неустойчивая неподвижная точка.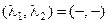 - устойчивая неподвижная точка (узел или фокус);
- устойчивая неподвижная точка (узел или фокус); - устойчивый предельный цикл.
- устойчивый предельный цикл.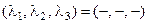 - устойчивая неподвижная точка;
- устойчивая неподвижная точка;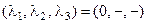 - устойчивый предельный цикл;
- устойчивый предельный цикл; - странный аттрактор.
- странный аттрактор.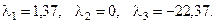
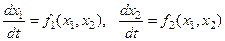 .
.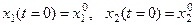 .
.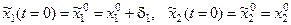 .
. .
. .
. .
. ,
,  ,
,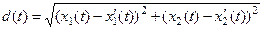 ,
, ,
,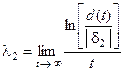 .
.
 .
.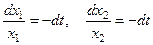 ;
; ;
; ;
;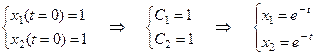
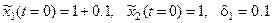 ;
;
 .
.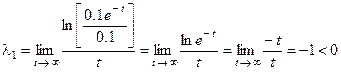 .
. ;
;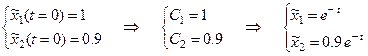
 .
. .
.


