Определение показателей ЛяпуноваВозьмём фазовую траекторию х (t) динамической системы (17.1), выходящую из точки х (0), а также траекторию, близкую к ней:
Рассмотрим функцию
определённую на векторах начального смещения При всевозможных поворотах вектора начального смещения по n направлениям в N- мерном фазовом пространстве функция (17.2) будет меняться скачками и принимать конечный ряд значений Сумма показателей Ляпунова есть средняя дивергенция потока фазовых траекторий, которая для диссипативной системы (т.е. системы, имеющей аттрактор) всегда должна быть отрицательной. Как показывают численные примеры, у некоторых диссипативных систем показатели Ляпунова инвариантны относительно всех перебранных начальных условий. Поэтому спектр показателей Ляпунова можно считать свойством аттрактора.
|
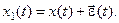
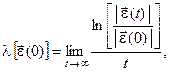(17.2)
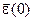таких, что 
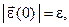где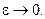 
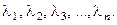Эти значения функции l называются показателями Ляпунова. Положительные показатели Ляпунова служат мерой среднего экспоненциального расхождения соседних траекторий, а отрицательные - мерой средней экспоненциальной сходимости траекторий к аттрактору.
