Пример 2.1
Рассмотрим пример обучения персептрона. При обсуждении его функционирования мы выяснили, что эта двухвходовая модель нейрона делит плоскость на две полуплоскости (см. рисунок 2.4). Соответственно, если мы разместим на плоскости два класса выборок, которые можно разделить при помощи прямой линии, то персептрон в процессе обучения должен найти эту линию. Для нашего испытания начертим эталонную прямую, обозначенную на рисунке 2.7 символом L. Предположим, что все точки плоскости, лежащие над этой прямой, представляют выборки класса 1, а точки, лежащие под прямой L, представляют класс 2. В обеих полуплоскостях расположено бесконечное множество точек, поэтому мы должны отобрать по несколько представителей каждого класса. Мы хотим, чтобы персептрон после обучения формировал на выходе сигнал «1» для выборок из первого класса и сигнал «-1» - для выборок, принадлежащих второму классу. Применяемая обучающая последовательность представлена в таблице 2.1,
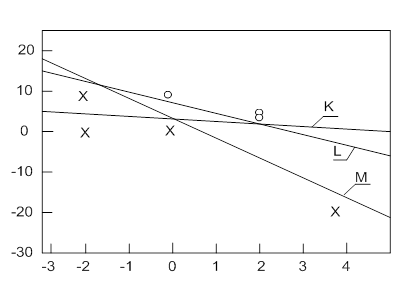
Рис. 2.7. Решающие границы для примера 2.1
Примем следующие начальные значения весов персептрона: w 1= 2, w2 = 2, θ = -4. На основании этих параметров и приведенных ранее данных чертим прямую К, которая показывает разделение пространства (решающую границу), найденную персептроном до начала процесса обучения. После 10 эпох выполнения алгоритма обучения (на входы нейрона 10 раз подавались все элементы обучающей выборки) персептрон начал корректно классифицировать входные сигналы, несмотря на то что прямая М не совпадает с прямой L. Таблица 2.1
|