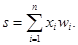Структуру и функционирование одиночного нейрона

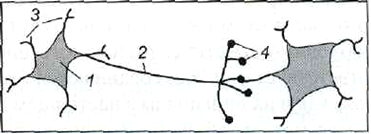
Базовый элемент нервной системы - нервная клетка, называемая нейро­ном. На рисунке 2.1 представлена упрощенная модель нейрона. В нейроне можно выделить тело клетки, называемое сомой, а также исходящие из него два вида отростков: а) по которым в нейрон поступает информация - дендриты и б) по которым нейрон передает информацию - аксон. Каждый нейрон имеет только один выходной отросток, по которому он может передавать импульс другим нейронам.

Рис. 2.1. Упрощенная модель нейрона и его соединения с соседним нейроном

1 - тело клетки; 2 - аксон; 3 - дендри­ты; 4 - синапсы

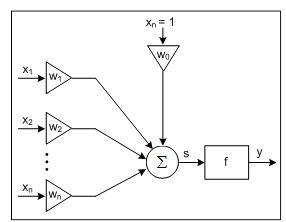
Одиночный нейрон принимает возбуждения от огромного количества нейронов (их число может достигать тысячи). Как уже отмеча­лось, мозг человека состоит из порядка 10¹¹ нейронов, которые взаимодейст­вуют через огромное количество соединений. Каждый нейрон передает воз­буждение другим нейронам через нервные стыки, называемые синапсами, при этом процесс передачи сигналов имеет сложную электрохимическую природу. Синапсы играют роль репитеров информации, в результате функци­онирования которых возбуждение может усиливаться или ослабляться. Как следствие, к нейрону приходят сигналы, одна часть из которых оказывает воз­буждающее, а вторая - тормозящее воздействие. Нейрон суммирует возбуж­дающие и тормозящие импульсы. Если их алгебраическая сумма превышает некоторое пороговое значение, то сигнал с выхода нейрона пересылается по­средством аксона к другим нейронам.

Рассмотрим модель нейрона, связанную с первыми попытками формали­зовать описание функционирования нервной клетки. Введем следующие обо­значения: п - количество входов нейрона; х_1,..., х_n - входные сигналы, х = [ х₁,…, х_n ]^T; w_0,…,w_n - синаптические веса, w =[w₀,..., w_n]^T; у - выходной сигнал нейрона; w₀ - пороговое значение; f - функция активации.

Формула, описывающая функционирование нейрона, имеет вид

y = f(s), (2.1)

где

Выражения (2.1) и (2.2) описы­вают нейрон, представленный на рисунке 2.2.

Рис. 2.2. Модель нейрона

Функция активации f мо­жет принимать различные формы в зависимости от конкретной модели нейрона.

Как следует из приведенных формул, нейрон функционирует очень простым образом. Вначале входные сигналы х₀, х_и...,х_п умно­жаются на соответствующие им веса w₀, w_x,..., w_n. Полученные значения суммируются. В результате возника­ет сигнал s, отражающий функцио­нирование линейной части нейрона. Этот сигнал подается на вход функции активации, которая чаще всего имеет нелинейный характер. Предположим, что значение сигнала

х₀ равно 1, а вес w₀ называется порогом (англ. bias). Где хранятся знания в нейроне, имеющем такое описание? Оказывается, что знания хранятся именно в весах. Однако наибольшим феноменом оказывает­ся то, что нейроны очень легко обучаются (при помощи алгоритмов, описы­ваемых в следующих разделах текущей главы), причем обучение сводится к подбору значений весов.

На рисунке 2.2 изображена обобщенная модель нейрона, однако в искусст­венных нейронных сетях применяются его конкретные модификации. Неко­торые частные модели нейрона будут обсуждаться в следующих разделах. Необходимо отметить, что искусственные нервные клетки, структура которых соответствует рисунке 2.2, соединяются между собой в математических моделях также как и их оригиналы в настоящем мозге. Способы соединения нейронов, а также методы обучения возникающих при этом структур мы также будем рассматривать в следующих разделах.