Какие алгоритмы нечеткого вывода Вы знаете? Стр 57
Алгоритм Мамдани (Mamdani). Алгоритм Мамдани является одним из первых, который нашел применение в системах нечеткого вывода. Он был предложен в 1975 г. Английским математиком Е. Мамдани (Ebrahim Mamdani) в качестве метода для управления паровым двигателем. По своей сути этот алгоритм порождает рассмотренные выше этапы, поскольку в наибольшей степени соответствует их параметрам. Формально алгоритм Мамдани может быть определен следующим образом. - Формирование базы правил систем нечеткого вывода. Особенности формирования базы правил совпадают с рассмотренными выше при описании данного этапа. - Фаззификация входных переменных. Особенности фаззификации совпадают с рассмотренными выше при описании данного этапа. - Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий каждого из правил нечетких продукций используются парные нечеткие логические операции. Те правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов. - Активизация подзаключений в нечетких правилах продукций. Осуществляется по формуле (6.4), при этом для сокращения времени вывода учитываются только активные правила нечетких продукций. - Аккумуляция заключений нечетких правил продукций осуществляется по формуле объединения нечетких множеств, соответствующих термам подзаключений, относящихся к одним и тем же выходным лингвистическим переменным. - Дефаззификация выходных переменных. Традиционно используется метод центра тяжести в форме (1.16).
Алгоритм Цукамото (Tsukamoto). Формально алгоритм Цукамото может быть определен следующим образом. - Формирование базы правил систем нечеткого вывода. Особенности формирования базы правил совпадают с рассмотренными выше при описании данного этапа. - Фаззификация входных переменных. Особенности фаззификации совпадают с рассмотренными выше при описании данного этапа. - Активизация подзаключений в нечетких правилах продукций. Осуществляется использованием формулы (1.12), посредством чего находится совокупность нечетких множеств: - Аккумуляция заключений нечетких правил продукций. Осуществляется по формуле объединения нечетких множеств, соответствующих термам подзаключений, относящихся к одним и тем же выходным лингвистическим переменным. - Дефаззификация выходных переменных. Может использоваться любой из рассмотренных выше методов дефаззификации. Алгоритм Сугено (Sugeno). Формально алгоритм Сугено, предложенный Сугено и Такаги, может быть определен следующим образом. - Формирование базы правил систем нечеткого вывода. В базе правил используются только правила нечетких продукции в форме:
ПРАВИЛО<#>:ЕСЛИ“
Здесь - Фаззификация входных переменных. Особенности фаззификации совпадают с рассмотренными выше при описании данного этапа. - Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий всех правил нечетких продукций, как правило, используется логическая операция min – конъюнкции. Те правила, степень истинности условий которых отлична от нуля, считается активными и используются для дальнейших расчетов. - Активизация подзаключений в нечетких правилах продукций. Во-первых, с использованием метода (1.12) находятся значения степени истинности всех заключений правил нечетких продукций. Во-вторых, осуществляется расчет обычных (не нечетких) значений выходных переменных каждого правила. Это выполняется с использованием формулы для заключения (1.20), в которую вместо - Аккумуляция заключений нечетких правил продукций. Фактически отсутствует, поскольку расчеты осуществляются с обычными действительными числами - Дефаззификация выходных переменных. Используется модифици-рованный вариант в форме метода центра тяжести для одноточечных множеств. Упрощенный алгоритм нечеткого вывода. Формально упрощенный алгоритм может быть определен следующим образом. Формирование базы правил систем нечеткого вывода. В базе правил используются только правила нечетких продукции в форме:
ПРАВИЛО <#>: ЕСЛИ “
Здесь Фаззификация входных переменных. Особенности фаззификации совпадают с рассмотренными выше при описании данного этапа. - Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий всех правил нечетких продукций, как правило, используется логическая операция min – конъюнкции. Те правила, степень истинности условий которых отлична от нуля, считается активными и используются для дальнейших расчетов. - Активизация подзаключений в нечетких правилах продукций. Осуществляется с использованием метода (1.13), посредством чего находятся значения степеней истинности всех заключений правил нечетких продукций - Аккумуляция заключений нечетких правил продукций. Фактически отсутствует, поскольку расчеты осуществляются с обычными действительными числами - Дефаззификация выходных переменных. Используется модифицированный вариант в форме метода центра тяжести для одноточечных множеств. При решении практических задач нечетких задач нечеткого моделирования могут одновременно использоваться несколько алгоритмов нечеткого вывода с целью получения наиболее адекватных результатов. Ниже рассматриваются примеры применения некоторых из этих алгоритмов в задачах нечеткого управления.
|

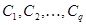 , где q— общее количество подзаключений в базе правил.
, где q— общее количество подзаключений в базе правил.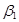 есть
есть 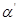 ”И“
”И“ 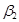 есть
есть 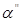 ”ТО“
”ТО“  ”. (1.20)
”. (1.20) - некоторые весовые коэффициенты. При этом значение выходной переменной w в заключении определяется как некоторое действительное число.
- некоторые весовые коэффициенты. При этом значение выходной переменной w в заключении определяется как некоторое действительное число. и
и  подставляются значения входных переменных до этап фаззификации. Тем самым определяются множество значений
подставляются значения входных переменных до этап фаззификации. Тем самым определяются множество значений  и множество значений выходных переменных
и множество значений выходных переменных  , где n— общее количество правил в базе правил.
, где n— общее количество правил в базе правил.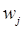 .
.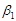 есть
есть 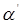 ” И “
” И “ 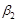 есть
есть  ” ТО “
” ТО “ 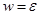 ”. (1.21)
”. (1.21)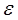 - некоторое действительное число.
- некоторое действительное число.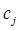 .
.


