Модель персептрона
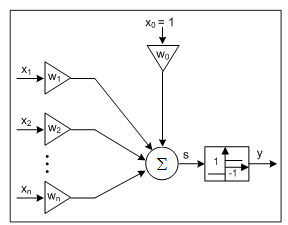
Структура персептрона представлена на рисунке 2.3.
Рис. 2.3. Структура персептрона
Функционирование персептрона можно описать выражением
Обратим внимание, что формула (2.3) сводится к более обобщенному выражению (2.1) при
В соответствии с функцией активации персептрон может принимать только два различных выходных значения, поэтому он может классифицировать сигналы, подаваемые на его вход в виде векторов х ~ [ х1..., хn ] T одному из двух классов. Например, одновходовый персептрон может распознавать, является входной сигнал положительным или отрицательным. При наличии двух входов персептрон разделяет плоскость на две полуплоскости. Такая декомпозиция задается прямой линией, определяемой уравнением
Уравнение (2.5) можно записать в виде
В общем случае, когда персептрон имеет п входов, он разделяет n - мерное пространство входных векторов х на два полупространства. Эти полупространства отделяются друг от друга (n - 1) - мерной гиперплоскостью, которая называется решающей границей (англ. decision boundary) и задается уравнением
На рисунке 2.4 представлена решающая граница для п = 2. Необходимо отметить, что прямая, разделяющая полуплоскости, всегда перпендикулярна вектору весов w = [ w 1, w 2]T. Как мы уже отмечали во введении, персептрон можно обучать. В процессе обучения модифицируются веса персептрона. Метод обучения персептрона получил название «обучение с учителем» или «обучение под надзором». Роль учителя заключается в подаче на вход персептрона сигналов x (t)= [ x 0(f), x 1 (t),..., хп(t) ] T, t = 1, 2,..., для которых известны истинные значения выходных сигналов d(t), t = 1,2, …, называемых эталонными сигналами.
Рис. 2.4. Решающая граница для n=2
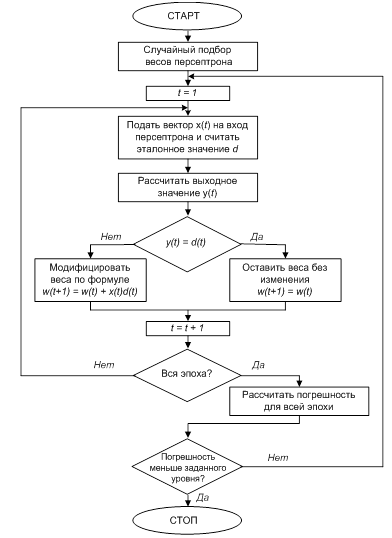
Совокупность таких входных выборок соответствующих им значений эталонных сигналов называется обучающей последовательностью. При использовании методов рассматриваемой группы после ввода входных значений рассчитывается выходной сигнал нейрона. После этого веса модифицируются так, чтобы минимизировать погрешность между эталонным сигналом и выходным сигналом персептрона. Такой подход объясняет термин «обучение с учителем», поскольку именно учитель задает эталонные значения. Конечно, существуют алгоритмы обучения сетей без учителя, однако эти алгоритмы мы будем рассматривать несколько позднее. Предлагаемый в настоящий момент алгоритм обучения персептрона состоит из следующих шагов: 1. Присвоить начальным весам персептрона случайные значения. 2. На входы нейрона подать обучающий вектор х = x (t)= [ x0 (t), x1 (t),..., xn (t)] T, t = 1,2,…. 3. Рассчитать выходное значение персептрона у по формуле (2.3). 4. Сравнить выходное значение у (t) с эталонным значением d=d (x (t)) , 5. Модифицировать веса следующим образом: а) если y (x (t)) ≠ d (x (t), то wi (t +1) = wi (t) +d (x (t)) xi (t); б) если y (x (t))= d (x (t)), то wi (t +1) = wi (t), т.е. значения весов не изменяются. 6. Перейти к шагу 2. Выполнение алгоритма продолжается до тех пор, пока для всех входных векторов, входящих в состав обучающей последовательности, погрешность на выходе не станет меньше априори заданного уровня. На рисунке 2.5 представлена блок-схема обучения персептрона. Выполнение одного внутреннего цикла этой схемы соответствует одной так называемой эпохе, которую составляют данные, образующие обучающую последовательность. Выполнение внешнего цикла отражает возможность многократного применения одной и той же обучающей последовательности, пока не будет выполнено условие остановки алгоритма.
Рис. 2.5. Блок-схема алгоритма обучения персептрона
. Докажем, что алгоритм обучения персептрона сходится. Теорема о сходимости персептрона формулируется следующим образом: Если существует набор весов w*=[ w 1*,..., wn* ] T, корректно классифицирующий обучающие векторы х =[ x 1 ,..., хп ] T, т.е. выполняющий отображение у=d (x), то обучающий алгоритм найдет решение за конечное количество итераций при любых начальных значениях вектора весов w. Предположим, что обучающая выборка представляет линейно сепарабельные классы, поскольку персептрон можно обучить только в этом случае. Покажем, что существует конечное количество шагов модификации весов, после выполнения которых персептрон будет корректно выполнять отображение у=d( x ). Поскольку функция активации персептрона имеет тип «sgn», длина вектора w * может быть произвольной, например, равной 1,т.е. || w*|| = 1. Поэтому в процессе обучения вектор w достаточно модифицировать так, чтобы показанный на рисунке 2.6. угол α был равен 0. Очевидно, в этом случае cos (α) = 1. Из факта, что | w * ° х | > 0 (символ «о» обозначает скалярное произведение векторов) и w * является решением, следует существование такой константы δ > 0, для которой | w *° х| > δ при любых векторах х, входящих в обучающую последовательность
Рис. 2.6. Иллюстрация выполнения алгоритма обучения персептрона для n=2
Из определения скалярного произведения следует, что
Поскольку
то
В соответствии с алгоритмом обучения персептрона веса для заданного входного вектора х модифицируются согласно формуле w ' = w + Δ w, где Δ w = d (х) х. Мы предполагаем, что на выходе появится ошибка и что коррекция весов будет необходима. Заметим, что w '° w * = w ° w * +d( x ) w * ° х, (2.11) поэтому
w ' ° w * = w ° w * + sgn(w *° x) w *° x. (2.12)
Истинны следующие суждения:
а) если w *° х < 0, то sgn(w *° x) = -l, поэтому sgn(w *° x) w *° х = -l(w *° x) >0;
б) если w * ° х > 0,тo sgn(w * ° x) = 1, поэтому sgn(w * ° х) w * ° х = l(w * ° х) > 0.
Следовательно, sgn(w * ° х) w * ° х = | w *° х|. (2.13)
В соответствии с формулами (2.12) и (2.13) можно записать:
w ' ° w * = w ° w * + | w *° х|. (2.14)
Нам также известно, что |w*° х | > δ, поэтому
w ' ° w * > w ° w * + δ. (2.15)
Теперь оценим значение || w '||2, не забывая о том, что мы рассматриваем случай, когда при подаче на вход обучающего вектора х на выходе сети появляется ошибка, т.е. d(x)=-sgn(w ° x). (2.16) Очевидно, что
|| w '||2 =||w + d (x) x ||2 ||w|| + 2 d (x) w ° x +|| x ||2. (2.17)
С использованием зависимостей (6.16) и (6.17), а также предполагая ограниченность входных сигналов, получаем
|| w '||2 < || w ||2 + || x ||2 = || w ||2 + C. (2.18) После t шагов модификации весов сети зависимости (6.15) и (6.18) принимают вид
w (t) ° w * > w ° w * + t δ; (2.19)
|| w (t)||2 < || w ||2 + tC. (2.20)
С использованием формул (2.10), (2.19) и (2.20) получаем
Поэтому должны существовать такие значения t = t max, для которых cos(α) = 1. Следовательно, существует конечное количество шагов модификации весов, после которых вектор начальных весов будет корректно выполнять отображение у = d( x ). Если предположить, что начальные значения весов равны 0, то
t max =С/δ2. (2.22)
|

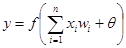 . (2.3)
. (2.3)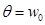 .Функция f может быть дискретной ступенчатой функцией - биполярной (т.е. принимающей значения -1 или 1) либо униполярной (принимающей значения 0 или 1). В последующих рассуждениях будем предполагать, что функция активации биполярная и имеет форму
.Функция f может быть дискретной ступенчатой функцией - биполярной (т.е. принимающей значения -1 или 1) либо униполярной (принимающей значения 0 или 1). В последующих рассуждениях будем предполагать, что функция активации биполярная и имеет форму
 . (2.4)
. (2.4) . (2.5)
. (2.5) (2.6)
(2.6)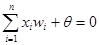 . (2.7)
. (2.7)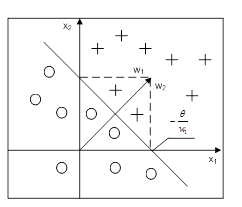

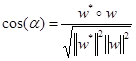 . (2.8)
. (2.8)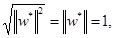 (2.9)
(2.9) (2.10)
(2.10)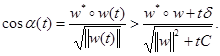 (2.21)
(2.21)


