Дайте определение операции импликации.
В традиционной логике материальная импликация → определяется как логическая связка для пропозициональных переменных. Так, если А и В – пропозициональные переменные, то таблица истинности для А → В, или, что эквивалентно, ЕСЛИ А, ТО В, записывается в таком виде
В обычных рассуждениях, однако, выражение ЕСЛИ А, ТО В употребляется в ситуациях, в которых А и В – нечеткие множества, а не пропозициональные переменные. Например, в случае высказывания ЕСЛИ Джон болен, ТО Джон капризен, которое можно сокращенно записать как болен → капризен, болен и капризен в сущности – названия нечетких множеств. То же самое справедливо по отношению к высказыванию ЕСЛИ яблоко красное, ТО яблоко спелое, где красное и спелое играют роль нечетких множеств. Чтобы обобщить понятие материальной импликации на нечеткие множества, предположим, что U и V – два возможно различных универсальных множества, а A, B и C – нечеткие подмножества U, V и V соответственно. Сначала определим смысл высказывания ЕСЛИ А, ТО В, ИНАЧЕ С и затем определим ЕСЛИ А, ТО В как частный случай высказывания ЕСЛИ А, ТО В, ИНАЧЕ С. Высказывание ЕСЛИ А, ТО В, ИНАЧЕ С есть бинарное нечеткое отношение в U
ЕСЛИ А, ТО В, ИНАЧЕ С = А
То есть если A, B и C – унарные нечеткие отношения в U, V и V, тогда ЕСЛИ А, ТО В, ИНАЧЕ С – бинарное нечеткое отношение в U
ЕСЛИ А, ТО В = ЕСЛИ А, ТО В, ИНАЧЕ V = A
В сущности это равнозначно интерпретации высказывания ЕСЛИ А, ТО В высказыванием ЕАЛИ А, ТО В, ИНАЧЕ безразлично. Полезно заметить, что в терминах матриц отношения А, В и С равенство (1.5) можно выразить как сумму попарных произведений, содержащих А и В (и
ЕСЛИ А, ТО В, ИНАЧЕ C=[A] [B] + [
Пример 1.6. Проиллюстрируем (1.5) и (1.6) следующим примером. Предположим, что U = V = 1 + 2 + 3, А = малый = 1/1 + 0.4/2, В = большой = 0.4/2 + 1/3, С = не большой = 1/1 + 0.6/2. Тогда ЕСЛИ А, ТО В, ИНАЧЕ C= (1/1 + 0.4/2) = 0.4/(1,2) + 1/(1,3) + 0.6/(2,1) + 0.6/(2,2) + 0.4/(2,3) + 1/(3,1) + 0.6/(3,2), что можно представить в виде матрицы отношения
ЕСЛИ А, ТО В, ИНАЧЕ С = Аналогично
ЕСЛИ А, ТО В = (1/1 + 0.4/2)
или, эквивалентно, ЕСЛИ А, ТО В =
|

 V, определяемое следующим образом:
V, определяемое следующим образом:
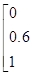
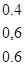
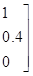 . (1.7)
. (1.7)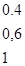
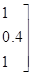 . (1.8)
. (1.8)


