Пример2.2

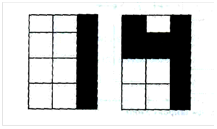
Рассмотрим пример обучения нейрона с применением правила Хебба в версии с учителем. Задача заключается в такой модификации весов нейрона, чтобы он мог различать цифры 1 и 4, схематически изображенные на рисунке 2.13. Если белым полям на этом рисунке сопоставить значение I, а черным полям - значение -1, то получим два вектора, входящих в состав обучающей последовательности:­

 

[-1 -1 1 -1 -1 1 -1 -1 1 -1 -1 1] – для цифры 1;

[1 -1 1 1 1 1 -1 -1 1 -1 -1 1] – для цифры 4.

 

Применительно к первому образцу (цифра 1) нам необходимо, чтобы на выходе нейрона появлялся сигнал d = -1, а для второго образца (цифра 4) эта­лонный выходной сигнал должен быть равен d = 1. Поскольку у нас есть вход­ные и выходные эталоны, то веса нейрона на каждой итерации будут модифи­цироваться в соответствии с выражением (2.94). Начальные значения весов равны 0. Нейрон с функцией активации типа «signum» будет обучаться на протяжении 100 эпох, коэффициент обучения выбран равным 0,2. После обу­чения нейрона и подачи на его вход первого обучающего вектора на выходе

Рис. 2.13. Иллюстрация к примеру 2.2

 

появляется сигнал s = -120, а при подаче на вход второго обучающего вектора на выходе появляется сигнал s = 120. Можно предположить, что с увеличением количества эпох эти значения также будут возрастать. Вектор весов после обучения принял вид: w = [40 00 40 40 000000 0]. Мы видим, что изменениям подверглись только те компоненты вектора весов, которые соот­ветствовали различным значениям конкретных компонент обучающих после­довательностей.

28. Чем отличается обучение отдельного нейрона от обучения нейронной сети?

В предыдущем параграфе было показано, что нейроны могут обучаться, помимо то­ то­го, при описании персептрона мы по­казали, что при наличии п входов он может декомпозировать n-мерное пространство на два подпространст­ва. Эти подпространства разделяют­ся (п- 1)-мерной гиперплоскостью. Область задач, которые может решать одиночный персептрон, достаточно узкая. В ка­честве примера можно привести задачу реализации логической фун­кции «исключенное ИЛИ» - XOR. Обучающая последовательность для решения этой задачи представлена в таблице 2.2.

Таблица 2.2

Обучающая последовательность для задачи XOR

 

x1	x2	d = XOR (x1,x2)
+1 +1 -1 -1	+1 -1 +1 -1	-1 +1 +1 -1

 

На рисунке 2.14 показаны значения обучающей последовательности из таблице 2.2. Из рисунка следует, что не существует прямой, которая отдели­ла бы точки со значениями функции XOR, равными -1, от точек со зна­чениями, равными 1. В этом случае роль решающей границы играет эл­липс, поэтому алгоритм, изображен­ный на рисунке 2.5,

Рис. 2.14. Иллюстрация к задаче XOR

 

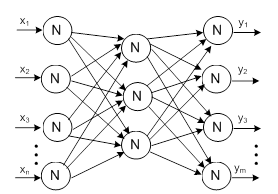
оказывается не сходящимся. Мы не можем подобрать веса одиночного персептрона так, чтобы он корректно решал задачу XOR. На помощь приходят многослойные сети. Мы вновь обратимся к задаче XOR при обсуждении методов обучения этих сетей. Что представляют собой многослойные сети? Это взаимосвязанные нейроны, размещенные в двух или более слоях. Как правило, используются нейроны с сигмоидой на выходе, однако могут применяться и нейроны с дру­гими функциями активации - например, линейными, которые чаще всего встречаются в последних слоях нейронной сети. Многослойные нейронные сети должны содержать, как минимум, два слоя: входной и выходной. Между ними могут располагаться скрытые слои. Если сеть содержит только два слоя, то входной слой отождествляется со скрытым слоем. В некоторых пуб­ликациях входным слоем называется вектор входных сигналов, подаваемых на нейронную сеть. В рассматриваемых нами структурах сигналами обмени­ваются только нейроны, расположенные в различных слоях.

В пределах одно­го и того же слоя нейроны не могут взаимодействовать друг с другом. Сигна­лы передаются от входного слоя к выходному слою (это объясняет название «однонаправленная сеть»), причем обратные связи с предыдущими слоями отсутствуют. Типовая структура однонаправленной трехслойной сети изоб­ражена на рисунке 2.15.

В следующих разделах мы рассмотрим различные алгоритмы обучения мно­гослойных сетей с учителем. Вначале будет представлен алгоритм обратного распространения ошибки (англ. error backpropagation), а также несколько его модификаций. Следующим будет обсуждаться алгоритм RLS. Далее мы покажем, какое влияние оказывает подбор соответствующей структуры сети на процессы обучения и функционирования нейронной сети. Как отмечалось ранее, представленные в настоящей главе алгоритмы реализуют обучение с учителем, иначе называемое обучением под надзором.

Рис. 2.15. Структура трехслойной нейронной сети

 

Напомним, что озна­чает этот термин. При использовании обсуждаемых алгоритмов мы предпо­лагаем, что обучающая последовательность состоит из пар, каждая из которых содержит вектор входных значений и вектор эталонных выходных сигналов.

Обучение реализуется следующим образом: вначале входные значения из обучающей последовательности подаются на вход сети, после чего последо­вательно рассчитываются выходные значения каждого нейрона от входного до выходного слоя. Таким способом выясняется реакция сети на сигнал (обра­зец), поступивший на ее вход. Поскольку нам известно, каким должно быть выходное значение (оно содержится в обучающей последовательности), мы будем стараться так модифицировать веса сети, чтобы выходное значение максимально приближалось к эталонному значению. В этом заключается суть алгоритмов рассматриваемого класса, поскольку «учитель» указывает, какой должна быть реакция сети.