Алгоритм обратного распространения ошибки
При рассмотрении различных моделей нейронов мы обсуждали основные технологии их обучения. Чаще всего обучение осуществлялось следующим образом. Рассчитывалась сумма произведений входных сигналов на соответствующие им веса. Далее полученное значение подавалось на вход используемой функции активации, на выходе которой появлялся выходной сигнал нейрона. Поскольку требуемое выходное значение нам известно (оно равно эталонному выходному значению, содержащемуся в обучающей выборке), то погрешность сигнала на выходе нейрона определяется достаточно просто. Искомая погрешность равна разности между фактическим выходным значением и эталонным значением. Аналогичным образом можно рассчитать погрешность для последнего слоя в многослойных сетях. Однако в этой ситуации возникает сложность с расчетом погрешности для скрытых слоев, поскольку учитель не знает эталонные значения на выходах расположенных в них нейронов. На помощь приходит наиболее распространенная технология обучения многослойных нейронных сетей, называемая методом обратного распространения ошибки. Для описания этого алгоритма необходимо формально определить соответствующую меру погрешности. Она представляет собой функцию, в которой в роли переменных выступают все веса многослойной нейронной сети. Обозначим искомую функцию Q(w), где w - вектор всех весов сети. В процессе обучения будем стремиться минимизировать значение Q (w) относительно вектора w. Разложим функцию Q(w) в ряд Тейлора в непосредственной близости от известного фактического решения w. Разложение в направлении р представим следующим образом:
Q (w+p)= Q (w)+[g(w)]Tp+0,5 p TH(w)p +..., (2.95)
где g (w) обозначает вектор градиента, т.е.:
a H(w) - гессиан, т.е. матрица вторых производных:
Веса модифицируются по формуле
w(t+1) = w(t) + η(t)p(t), (2.98)
где η - коэффициент обучения (способ подбора значения этого параметра будет описан несколько позднее). Веса могут модифицироваться так долго, пока функция Q не достигнет минимума либо ее значение не станет меньше априори заданного порога. Таким образом, задача сводится к поиску вектора направления р, обеспечивающего уменьшение погрешности на выходе сети на очередных шагах алгоритма. Это означает, что на следующих итерациях должно выполняться неравенство Q( w (t + 1))< Q (w(t)). Ограничим ряд Тейлора, аппроксимирующий функцию погрешности Q, линейным разложением, т.е.
Q (w+ p) = Q (w) + [g(w)]Tp. (2.99)
Поскольку функция Q( w ) зависит от весов, найденных на шаге t, a Q( w+р) - от весов, найденных на шаге (t+ 1 ) то для выполнения неравенства Q( w (t+1))<Q( w (t) достаточно подобрать вектор р(t), при котором g(w(t)Tp(t)<0. Легко заметить, что это условие выполняется при
p(t)=-g(w(t)). (2.100) При подстановке зависимости (2.100) в формулу (2.98) получаем следующее выражение для изменения весов многослойной нейронной сети:
w (t+ l)= w (t) - ηg(w (t)). (2.101) Зависимость (2.101) известна в литературе под названием «правило наискорейшего спуска». Для эффективного использования выражения (2.101) с целью вывода алгоритма обратного распространения ошибки необходимо формально описать структуру многослойной нейронной сети и ввести соответствующие обозначения. Эта структура изображена на рисунке 2.16. В каждом слое расположено Nk элементов, k =1,..., L, обозначаемых Nki, i = 1, ..., Nk. Элементы Nki будем называть нейронами, причем каждый из них может иметь сигмоиду на выходе. Обсуждаемая нейронная сеть имеет N0 входов, на которые подаются сигналы х1 (t), ...,xN0 (t), записываемые в векторной форме как
x = [ x 1(t),..., xN0 (t)]T, t = 1,2,.... (2.102)
Рис.2.16. Многослойная нейронная сеть
Выходной сигнал i -го нейрона в k- мслое обозначается уi(k)(t), i = 1,. .,Nk, k = 1,..., L. На рисунке 2.17 показана детальная структура i -го нейрона в k- мслое.
Рис. 2.17. Структура нейрона
Нейрон Nki имеет Nk входов, образующих вектор
причем xi(k)(t) = +1 для i = 0 и k = 1, ...,L. Обратим внимание на факт, что входной сигнал нейрона Nki связан с выходным сигналом (k - 1)-го слоя следующим образом:
 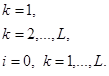 (2.104) (2.104)
На рисунке 2.17 символом wij(k) (t) обозначен вес входа i -го нейрона, i=1,…Nk, расположенного в k -м слое, который соединяет этот нейрон с j -м входным сигналом xi(k)(t), j= 0,1 ,...,Nk. Вектор весов нейрона Nki будем обозначать
Выходной сигнал нейрона Nki в момент t, t = 1,2,... определяется как
причем
Отметим, что выходные сигналы нейронов L -го слоя
одновременно являются выходными сигналами сети в целом. Они сравниваются с так называемыми эталонными сигналами сети
Погрешность на выходе сети определяется следующим образом:
При использовании зависимостей (2.101) и (2.110) получаем
Обратим внимание, что
Если ввести обозначение
то получим равенство
При этом алгоритм (2.111) принимает вид
Способ расчета значения
Для произвольного слоя k ≠ L получаем
Определим погрешность для i -го нейрона в k -м (не последнем) слое в виде
При подстановке выражения (2.118) в формулу (2.117) получаем
В результате алгоритм обратного распространения ошибки можно записать в виде
Мы рассмотрели последовательность математических выражений, описывающих способ обучения многослойной нейронной сети. Выполнение алгоритма начинается с подачи обучающей последовательности на вход сети. Вначале эта последовательность обрабатывается нейронами первого слоя. Конечно, под «обработкой» мы понимаем здесь расчет значений выходных сигналов (см. формулы (2.106), (2.107)) для каждого нейрона этого слоя. Полученные сигналы подаются на входы нейронов следующего слоя. Описанный цикл повторяется, т.е. вновь рассчитываются выходные сигналы нейронов очередного слоя, которые передаются далее - вплоть до выходного слоя. После получения выходного сигнала последнего слоя и выбора соответствующего эталонного сигнала из обучающей последовательности рассчитывается погрешность на выходе сети по формуле (2.121). Веса нейронов последнего слоя можно модифицировать при помощи дельта-правила также как и веса одиночного нейрона с сигмоидой на выходе - для этого используются формулы (2,121), (2.123), (2,124). Однако этот способ непригоден для модификации весов нейронов в скрытых слоях, поскольку значения для этих нейронов 27. Принцип обучения нейронной сети «без учителя»
|

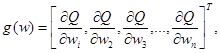 (2.96)
(2.96) (2.97)
(2.97)

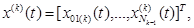 (2.103)
(2.103)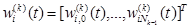 , k =1,..., L, i = 1 ..,,Nk. (2.105)
, k =1,..., L, i = 1 ..,,Nk. (2.105)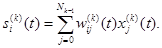 (2.107)
(2.107) (2.108)
(2.108) (2.109)
(2.109)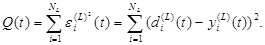 (2.110)
(2.110)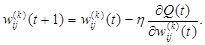 (2.111)
(2.111) (2.112)
(2.112)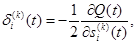 (2.113)
(2.113)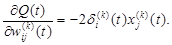 (2.114)
(2.114) (2.115)
(2.115)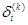 зависит от номера слоя. Для последнего слоя получаем
зависит от номера слоя. Для последнего слоя получаем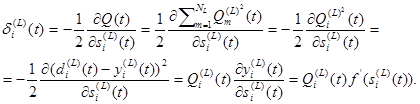 (2.116)
(2.116)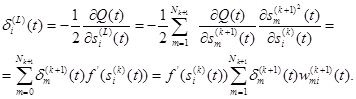 (2.117)
(2.117)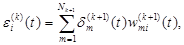 k = 1,…,L - 1. (2.118)
k = 1,…,L - 1. (2.118)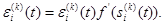 (2.119)
(2.119)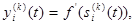
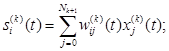 (2.120)
(2.120)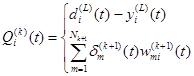

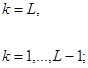
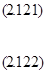
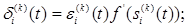 (2.123)
(2.123)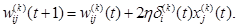 (2.124)
(2.124)


