Композиционное правило вывода
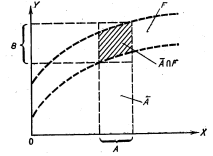
Основным правилом в традиционной логике является правило modus ponens, согласно которому мы можем судить об истинности высказывания В по истинности высказывания А и импликации А → В. Например, если А – высказывание «Джон в госпитале», то В – высказывание «Джон болен», то если истинно высказывание «Джон в госпитале», то истинно и высказывание «Джон болен» [6]. Во многих привычных рассуждениях правило modus ponens используется не в точной, а в приближенной форме. В отличи от традиционной логики при приближенных рассуждениях главным инструментом будет не правило modus ponens, а так называемое композиционное правило вывода, частным случаем которого является правило modus ponens. Композиционное правило вывода – это всего лишь обобщение следующей знакомой процедуры. Предположим (см. рисунок 1.6), что имеется кривая y=f(x), а также то, что: x=a, y=f(x), x=a, y=b=f(a). Обобщим теперь этот процесс (см. рисунок 1.7), предположив, что a – интервал, а f(x) – функция, значения которой суть интервал y=b, соответствующий интервалу a, мы сначала построим цилиндрическое множество a’ с основанием a и найдем его пересечение I с кривой, значения которой суть интервалы. Затем спроектируем это пересечение на ось OY и получим желаемое значение y в виде интервала b. Чтобы продвинуться еще на один шаг предположим, что A – нечеткое множество оси OX, а F – нечеткое отношение в OX
Рис. 1.6..Вывод y=bиз предпосылок x=aи y=f(x)
Рис. 1.7. Иллюстрация композиционного правила вывода в случае переменных со значениями-интервалами
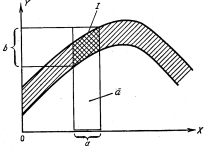
Проектируя затем это множество на осьOY. Таким образом, из того, что y=f(x)и x=A– нечеткое подмножество оси OX, мы получим значение yв виде нечеткого подмножества Bоси OY. Более конкретно, пусть μA, μA’, μF иμBобозначают функции принадлежности множеств A, A’, FиBсоответственно. Рис. 1.8. Иллюстрация композиционного правила вывода для нечетких переменных Тогда по определению множество А
и, следовательно,
Проектируя множество
т.е. выражение для функции принадлежности проекции B= A°F,
т.е. операция композиции сводится к максминному произведению матриц. Пример 1.5. Предположим A и F имеют вид
А = 0.2/1 + ½ + 0.3/3
и F = 0.8/(1,1) + 0.9/(1,2) + 0.2/(1,3) + 0.6/(2,1) + 1.0/(2,2) + 0.4/(2,3) + 0.5/(3,1) + 0.8/(3,2) + 1.0/(3,3). Выражая А и F с помощью матриц и образуя матричное произведение, получим
Вышеизложенное замечание и примеры помогают обосновать следующее правило вывода. Пусть U и V – два универсальных множества с базовыми переменными u и v соответственно. Пусть R(u), R(u,v) и R(v) обозначают ограничения на u, (u,v) и v соответственно и представляют собой нечеткие отношения в U, U R(u) = A, R(u,v) = F Имеет вид R(v) = A°F,
где A°F– композиция Aи F. В этом смысле мы можем делать вывод R(v) = A°Fиз того, что R(u) = Aи R(u,v) = F. В качестве простой иллюстрации применения этого правила предположим, что U= V= 1 + 2 + 3 + 4,
A= малый = 1/1 + 0.6/2 + 0.2/3 F= примерно равны = 1/(1,1) + 1/(2,2) + 1/(3,3) + 1/(4,4) + + 0.5/((1,2) + (2,1) + (2,3) + (3,2) + (3,4) + (4,3)). Другими словами, А - унарное нечеткое отношение в U, называемое малый, F– бинарное нечеткое отношение в U Уравнения назначения в этом случае имеют вид R(u) = малый, R(u,v) = примерно равны, и, следовательно, R(v) = малый °примерно равны =
что можно аппроксимировать следующим образом:
R(v) = более или менее малый, если терм более или менее определяется как оператор увеличения нечеткости, где K(1) = 1/1 + 0.7/2, K(2) = 1/4 + 0.7/3, K(3) = 1/3 + 0.7/4, K(4) = 1/4. Заметим, что применение этого оператора к R(u) дает [1 0.7 0.42 0.14] в качестве аппроксимации набора [1 0.6 0.5 0.2]. Итак, используя композиционное правило вывода, из того, что R(u) = малый и R(u,v) = примерно равны, мы вывели, что
R(v) = [1 0.6 0.5 0.2] точно
и R(v) = более или менее малый – в качестве лингвистического приближения. Словами этот приближенный вывод можно записать в виде
u – малый предпосылка u и v – примерно равны предпосылка v – более или менее малый приближенный вывод.
|

 OY. Вновь образуя цилиндрическое нечеткое множество A’ и его пересечение с основанием A и его пересечением с нечетким отношением F (см. рисунок 1.8). мы получим нечеткое множество
OY. Вновь образуя цилиндрическое нечеткое множество A’ и его пересечение с основанием A и его пересечением с нечетким отношением F (см. рисунок 1.8). мы получим нечеткое множество 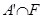 , которое является аналогом точки пересечения Iна рисунке 1.8.
, которое является аналогом точки пересечения Iна рисунке 1.8.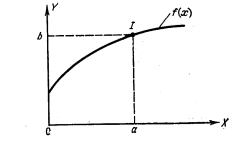
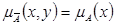
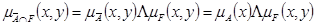
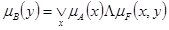
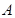
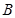
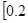
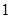
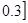 ·
· 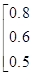
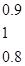
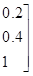 =
= 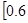
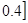
 V и V. Пусть A и F – нечеткие подмножества множеств U и U
V и V. Пусть A и F – нечеткие подмножества множеств U и U 



