Подавление шумов
Наблюдаемое изображение часто бывает искажено шумами и помехами различного физического происхождения: шумами видеодатчика, шумами зернистости фотоматериалов, ошибками в каналах передачи информации и др. При математическом описании искаженных изображений чаще всего используют аддитивный, импульсный и мультипликативный типы шумов. Если идеальное (незашумленное) изображение обозначить
где Импульсный шум проявляется на изображении в виде отдельных точек с максимальной (белой) или минимальной (черной) яркостью. Белые точки часто называют “солевым шумом”, а черные – “перечным шумом”.
Изображение
где
В MATLAB Image Processing Toolbox зашумление изображения различными типами шума осуществляется функцией imnoise. В зависимости от вида шума функция может иметь разные форматы:
1) аддитивный гауссовский шум
J = imnoise(I,'gaussian',m,v), где J – зашумленное изображение; I – исходное изображение; m – среднее значение шума (по умолчанию 0); v – дисперсия шума (по умолчанию 0.01);
2) импульсный шум (“соль и перец”)
J = imnoise(I,'salt & pepper',d),
где d – плотность шума, т. е. отношение числа поврежденных точек изображения к общему числу точек (по умолчанию 0.05); 3) мультипликативный шум J = imnoise(I,'speckle',v),
где v – дисперсия шума Как правило, шумы проявляются в виде разрозненных изменений отдельных элементов изображения и искаженные элементы могут заметно отличаться от соседних. На практике используются различные алгоритмы подавления шумов с помощью локальных операторов сглаживания (усреднения), являющихся по существу низкочастотными фильтрами. Элементы изображения
где
Матрицы нормированы для получения единичного коэффициента передачи, чтобы процедура подавления шума не вызывала смещения средней яркости обработанного изображения. Существуют маски бóльших размеров (5×5, 7×7 и т.д.), но они используются реже. В MATLAB Image Processing Toolbox фильтрация изображений шумоподавляющими масками может быть реализована с помощью функции imfilter, которая вызывается следующим образом: J = imfilter(I,H),
где J – профильтрованное изображение; H – маска фильтра; I – исходное изображение. Маски фильтров, приведенных в выражениях (5), в системе MATLAB задаются следующим образом:
H = [1 1 1; 1 1 1; 1 1 1]/9, H = [1 1 1; 1 2 1; 1 1 1]/10, H = [1 2 1; 2 4 2; 1 2 1]/16.
Побочным эффектом всех описанных выше линейных фильтров является то, что в результате усреднения на профильтрованном изображении Если наблюдаемое изображение повреждено аддитивным гауссовским шумом с нулевым средним и дисперсией
где В MATLAB Image Processing Toolbox подавление шума с помощью фильтра Винера осуществляется функцией wiener2, интерфейс которой имеет вид J = wiener2(I,[m n],noise), где J – профильтрованное изображение; I – наблюдаемое изображение; [m n] – размеры анализируемого участка изображения в пикселях по вертикали и горизонтали соответственно (по умолчанию – [3 3]); noise – мощность аддитивного шума (произведение дисперсии С помощью функций системы MATLAB мощность шума может быть вычислена как
noise = variance*prod(size(I)), где variance – дисперсия шума При вызове функции wiener2 параметр noise является необязательным. Если он не указан, то в качестве оценки дисперсии шума используется среднее значение всех локальных оценок Наиболее эффективным методом подавления импульсного шума (шума типа “соль и перец”) является медианная фильтрация. Это нелинейный метод обработки изображений, основанный на замене каждого элемента наблюдаемого изображения медианой всех элементов, попавших внутрь скользящего окна размером K × L, центр которого последовательно помещается в каждую точку изображения. (Медианой дискретной последовательности а 1, а 2, …, аN для нечетного N называется тот элемент последовательности, для которого существует (N –1)/2 элементов, не превышающих его по величине, и (N –1)/2 элементов, больше или равных ему по величине.) Медианный фильтр подавляет импульсные сигналы, длительность которых составляет менее половины ширины окна и вызывает уплощение вершины треугольных сигналов. Как правило, фильтр сохраняет контуры изображения, но иногда может искажать форму объектов. В частности, он скругляет острые (меньше 90º) углы ярких объектов на изображении. Медианная фильтрация изображений в MATLAB Image Processing Toolbox реализована в виде функции medfilt2, которая может быть вызвана следующим образом: J = medfilt2(I,[m n]),
где J – профильтрованное изображение; I – наблюдаемое изображение; [m n] – размеры скользящего окна в пикселях (по умолчанию – [3 3]).
2.2. Реставрация изображений
Реставрацией называют процесс компенсации искажений наблюдаемого изображения Пусть математическая модель искажений имеет вид двумерного линейного фильтра с импульсной характеристикой
где Если идеальное изображение рассматривается как реализация двумерного случайного процесса с нулевым средним и известным энергетическим спектром
где * – знак комплексного сопряжения. Оценка идеального изображения будет определяться как обратное двумерное преобразование Фурье произведения спектра наблюдаемого изображения и частотной характеристики реставрирующего фильтра, задаваемого выражением (8):
Если идеальное изображение не обладает пространственной корреляцией и его энергетический спектр принимает единичное значение во всем диапазоне пространственных частот
При отсутствии аддитивного шума винеровский фильтр вырождается в так называемый инверсный фильтр, имеющий частотную характеристику
В MATLAB Image Processing Toolbox реставрация изображений с помощью винеровского фильтра реализована в виде функции deconvwnr, интерфейс которой имеет вид
где Автокорреляционная функция идеального изображения может быть вычислена как
ICORR = fftshift(real(ifftn(abs(fftn(J.^2))),
где fftshift(…) – перегруппировка элементов матрицы спектральных коэффициентов, полученных в результате n -мерного преобразования Фурье таким образом, чтобы низкочастотные компоненты спектра занимали центральную часть матрицы; real(…) – вычисление действительной части комплексного числа; ifftn(…) – обратное n -мерное преобразование Фурье; abs(…) – вычисление абсолютной величины действительного или комплексного числа; fftn(…) – прямое n -мерное преобразование Фурье;.^2 – операция поэлементного возведения в квадрат всех элементов массива. Автокорреляционная функция аддитивного шума вычисляется аналогично. Параметры NCORR и ICORR являются необязательными. Если они не указаны, то функция deconvwnr реализует инверсный фильтр, определяемый выражением (11). Импульсные характеристики фильтров, моделирующих основные типы пространственных искажений, задаются в системе MATLAB с помощью функции fspecial. В зависимости от используемой модели искажений вызов функции может иметь следующий вид: 1) размытие контуров изображения за счет смещения камеры в процессе формирования изображения
h = fspecial('motion', len, theta), где h – импульсная характеристика фильтра; len – величина смещения в пикселях; theta – направление смещения в градусах, отсчитываемое относительно горизонтальной оси против часовой стрелки; 2) снижение резкости изображения путем усреднения значений яркости каждой точки по окрестности, имеющей форму диска
h = fspecial('disk', radius),
где radius – радиус диска (по умолчанию – 5 пикселей); формируемая матрица h имеет размеры [2*radius+1 2*radius+1]; 3) снижение резкости изображения путем свертки с дискретной аппроксимацией двумерной гауссоиды, вычисляемой по формуле
h = fspecial('gaussian', hsize, sigma),
где hsize – размеры формируемой матрицы h (по умолчанию – [3 3]); sigma – среднеквадратическое отклонение Для случаев, когда априорная информация о свойствах пространственных искажений и статистических характеристиках изображения и шума недоступна, были разработаны методы слепой реставрации. В MATLAB Image Processing Toolbox для слепой реставрации изображений используется функция deconvblind, позволяющая получить итеративное уточнение оценки идеального изображения и грубой оценки функции рассеяния точки. Функция может быть вызвана следующим образом:
[J,PSF] = deconvblind(I,INITPSF), где J – оценка идеального изображения Пример реставрации изображения описанными ранее методами с помощью функций, входящих в Image Processing Toolbox, приведен на рис. 2.
В качестве наблюдаемого изображения выбрано изображение биологических клеток живой ткани (см. рис. 1, а), искаженное фильтром типа ‘motion’ с параметрами len=31 и theta=11, к которому добавлен аддитивный гауссовский шум с дисперсией 0.002. При вычислении оценки идеального изображения методом слепой реставрации в качестве грубой оценки функции рассеяния использовалась матрица такого же размера, как и реальная функция рассеяния точки, состоящая из единиц. В MATLAB такую матрицу можно задать выражением
INITPSF = ones(size(PSF)).
2.3. Выделение контуров
Как правило, наиболее существенная информация о наблюдаемой сцене заключена в контурах изображения. Контуры содержат всю необходимую информацию о форме объектов, присутствующих на изображении, и операция выделения контуров очень часто облегчает последующий анализ наблюдаемой сцены (как визуальный, так и автоматический). Самым популярным методом выделения контуров является метод пространственного дифференцирования [2], основанный на оценке скорости изменения (градиента) яркости для каждой точки наблюдаемого изображения. Если яркость меняется достаточно быстро, то точка находится на границе двух областей разной яркости, т. е. принадлежит контуру. Оценка абсолютной величины градиента яркости для дискретного изображения может быть вычислена по правилу
где
Маски операторов Собеля и Превитта для выделения вертикальных перепадов яркости (вычисления Получаемый в результате массив
где Т – постоянный или меняющийся в зависимости от локальных свойств изображения порог. В результате получается бинарное изображение Главной причиной популярности методов, основанных на использовании масок пространственного дифференцирования, является простота их реализации на ЭВМ. Однако они чувствительны к шуму, присутствующему на изображении, и не могут гарантировать требуемый результат при обработке сложных естественных изображений. Для преодоления этих недостатков были разработаны методы выделения контуров, сочетающие в себе процедуры подавления шумов и анализа производных яркости более высокого порядка. Метод Марра-Хильдрета, например, совмещает в себе обе процедуры путем вычисления свертки изображения с пространственным фильтром, представляющим собой дискретную аппроксимацию лапласиана от гауссоиды:
где Наиболее совершенным методом выделения границ в MATLAB Image Processing Toolbox является кэнни-метод (от англ. “canny” – хитрый, умный), в котором изображение предварительно сглаживается шумоподавляющим фильтром в виде гауссоиды, а градиентное изображение вычисляется путем свертки сглаженного изображения с фильтром, имеющим вид первой производной от той же гауссоиды, которая использовалась для подавления шумов. Пороговая обработка градиентного изображения осуществляется с использованием двух порогов для выделения “сильных” и “слабых” границ. Точки “слабых” границ включаются в бинарное изображение Пример выделения контуров изображения различными методами приведен на рис. 3. В MATLAB Image Processing Toolbox выделение контуров на изображении осуществляется функцией edge. В зависимости от выбранного метода вызов функции может иметь следующий вид: выделение контуров с помощью масок Собеля, Превитта или Робертса
J = edge(I, method, thresh), где J – бинарное изображение 2) метод Марра-Хильдрета (с использованием лапласиана гауссоиды)
J = edge(I, 'log', thresh, sigma),
где sigma – среднеквадратическое отклонение 3) кэнни-метод
J = edge(I, 'canny', thresh, sigma),
где sigma – среднеквадратическое отклонение шумоподавляющего фильтра (по умолчанию 1). Порог thresh может быть задан либо в виде вектора [low high], либо скалярной величиной. В первом случае значение low используется для выделения слабых границ, а значение high – для выделения сильных. Во втором случае порог для выделения слабых границ вычисляется по правилу 0.4*thresh. Если порог не задан, то эти значения вычисляются автоматически на основе анализа статистических характеристик градиентного изображения
Качество контурного изображения, полученного с помощью различных методов выделения границ (Собеля, Превитта, Робертса, Марра-Хильдрета, кэнни), оценивается путем сравнения его с тестовым бинарным изображением
|

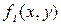 , то наблюдаемое изображение
, то наблюдаемое изображение  , искаженное аддитивным шумом, можно представить в виде
, искаженное аддитивным шумом, можно представить в виде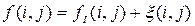 , (1)
, (1)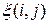 - случайная функция, закон распределения которой чаще всего является гауссовским с нулевым средним и дисперсией
- случайная функция, закон распределения которой чаще всего является гауссовским с нулевым средним и дисперсией 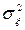 .
. (2)
(2) , (3)
, (3)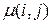 - случайная функция, закон распределения которой в дальнейшем примем равномерным с нулевым средним и дисперсией
- случайная функция, закон распределения которой в дальнейшем примем равномерным с нулевым средним и дисперсией 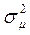 . Пример изображения, поврежденного различными типами шумов, приведен на рис. 1.
. Пример изображения, поврежденного различными типами шумов, приведен на рис. 1.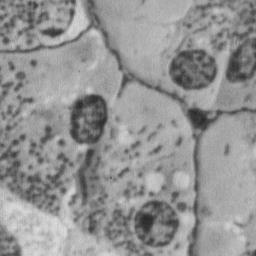
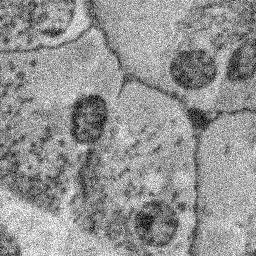

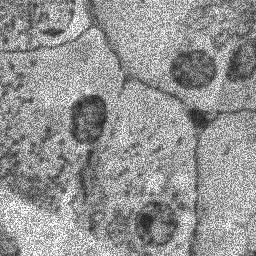
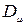 (по умолчанию 0.04).
(по умолчанию 0.04).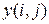 , получаемого в результате обработки исходного изображения
, получаемого в результате обработки исходного изображения  , (4)
, (4)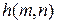 – элементы матрицы H. Подавление шумов обеспечивается низкочастотной фильтрацией с помощью матрицы
– элементы матрицы H. Подавление шумов обеспечивается низкочастотной фильтрацией с помощью матрицы 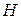 с положительными элементами. Наибольшее распространение получили следующие матрицы размерности 3×3, часто называемые шумоподавляющими масками:
с положительными элементами. Наибольшее распространение получили следующие матрицы размерности 3×3, часто называемые шумоподавляющими масками: (5)
(5) , то метод подавления шума на основе адаптивного фильтра Винера обеспечивает меньшую размытость контуров и мелких деталей по сравнению с описанными ранее методами. В соответствии с этим методом яркости точек профильтрованного изображения
, то метод подавления шума на основе адаптивного фильтра Винера обеспечивает меньшую размытость контуров и мелких деталей по сравнению с описанными ранее методами. В соответствии с этим методом яркости точек профильтрованного изображения  вычисляются на основе локальных оценок среднего значения
вычисляются на основе локальных оценок среднего значения 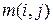 и дисперсии яркости
и дисперсии яркости 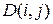 наблюдаемого изображения
наблюдаемого изображения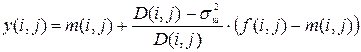 , (6)
, (6)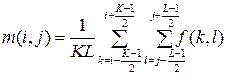 ;
; 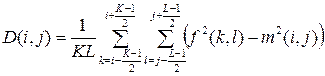 ; K и L – размеры анализируемого участка изображения по вертикали и горизонтали соответственно.
; K и L – размеры анализируемого участка изображения по вертикали и горизонтали соответственно.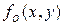 с целью получения оценки
с целью получения оценки 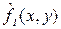 некоего идеального изображения
некоего идеального изображения  , которое наблюдалось бы на выходе идеального датчика, не вносящего никаких искажений. Искажения могут вноситься турбулентностью атмосферы, расфокусировкой оптики, недостаточным временем экспозиции, смещением датчика в процессе формирования изображения (размытость контуров наблюдаемых объектов) и т.п. Очевидно, что эффективность реставрации зависит от адекватности используемых моделей пространственных искажений. В литературе, посвященной цифровой обработке изображений, описание рассматриваемых ниже методов реставрации приводится для непрерывных изображений
, которое наблюдалось бы на выходе идеального датчика, не вносящего никаких искажений. Искажения могут вноситься турбулентностью атмосферы, расфокусировкой оптики, недостаточным временем экспозиции, смещением датчика в процессе формирования изображения (размытость контуров наблюдаемых объектов) и т.п. Очевидно, что эффективность реставрации зависит от адекватности используемых моделей пространственных искажений. В литературе, посвященной цифровой обработке изображений, описание рассматриваемых ниже методов реставрации приводится для непрерывных изображений 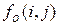 и
и 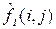 соответственно).
соответственно).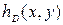 . Тогда частотная характеристика искажающего фильтра определяется как двумерное преобразование Фурье его импульсной характеристики
. Тогда частотная характеристика искажающего фильтра определяется как двумерное преобразование Фурье его импульсной характеристики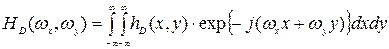 , (7)
, (7)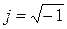 .
.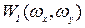 , а к искаженному изображению добавляется аддитивный гауссовский шум с нулевым средним и известным энергетическим спектром
, а к искаженному изображению добавляется аддитивный гауссовский шум с нулевым средним и известным энергетическим спектром  , то минимальная среднеквадратическая ошибка реставрации достигается использованием винеровского фильтра, частотная характеристика которого имеет вид
, то минимальная среднеквадратическая ошибка реставрации достигается использованием винеровского фильтра, частотная характеристика которого имеет вид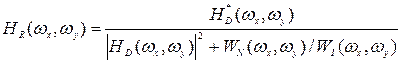 , (8)
, (8) . (9)
. (9)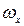 и
и  , то выражение (8) приобретает более простой вид:
, то выражение (8) приобретает более простой вид: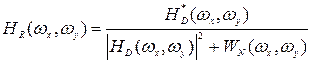 . (10)
. (10)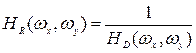 . (11)
. (11) = deconvwnr(I, PSF, NCORR, ICORR),
= deconvwnr(I, PSF, NCORR, ICORR),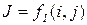 ;
;  – наблюдаемое изображение
– наблюдаемое изображение 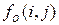 ; PSF – импульсная характеристика искажающей системы
; PSF – импульсная характеристика искажающей системы 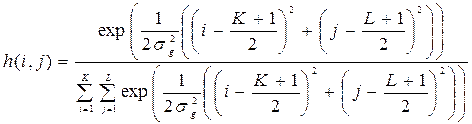
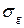 (по умолчанию – 0.5).
(по умолчанию – 0.5).


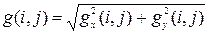 , (22)
, (22)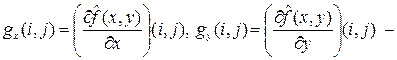 оценки частных производных, вычисляемые путем свертки массива исходных значений яркости
оценки частных производных, вычисляемые путем свертки массива исходных значений яркости 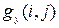 ) имеют вид:
) имеют вид: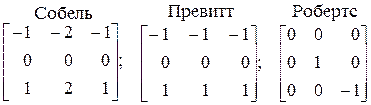 . (33)
. (33)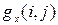 ) получаются из одноименных масок для выделения горизонтальных перепадов путем транспонирования, а маска оператора Робертса – поворотом на 90º по часовой стрелке.
) получаются из одноименных масок для выделения горизонтальных перепадов путем транспонирования, а маска оператора Робертса – поворотом на 90º по часовой стрелке.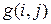 называют градиентным изображением. Далее осуществляется пороговая обработка градиентного изображения по правилу
называют градиентным изображением. Далее осуществляется пороговая обработка градиентного изображения по правилу , (44)
, (44)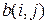 , единичные точки которого соответствуют потенциальным граничным точкам исходного изображения.
, единичные точки которого соответствуют потенциальным граничным точкам исходного изображения. , (55)
, (55) – среднеквадратическое отклонение гауссоиды;
– среднеквадратическое отклонение гауссоиды; 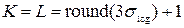 – размеры маски фильтра. Лапласиан (сумма вторых производных функции яркости по обеим координатам) обладает большей чувствительностью к перепадам яркости по сравнению с абсолютной величиной градиента, а использование гауссоиды для подавления шума позволяет повысить качество получаемого бинарного изображения, не внося существенных искажений в контурные линии исходного изображения.
– размеры маски фильтра. Лапласиан (сумма вторых производных функции яркости по обеим координатам) обладает большей чувствительностью к перепадам яркости по сравнению с абсолютной величиной градиента, а использование гауссоиды для подавления шума позволяет повысить качество получаемого бинарного изображения, не внося существенных искажений в контурные линии исходного изображения.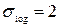 );
);





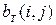 , единичные точки которого соответствуют тем точкам исходного изображения, которые были выделены как минимум тремя методами из пяти. Результат сравнения контурных изображений
, единичные точки которого соответствуют тем точкам исходного изображения, которые были выделены как минимум тремя методами из пяти. Результат сравнения контурных изображений 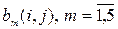 , сформированных указанными методами, выражается в виде числа
, сформированных указанными методами, выражается в виде числа  , вычисляемого по формуле
, вычисляемого по формуле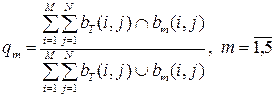 . (66)
. (66)


