Байесовский метод
Пусть на изображении выделен некоторый прямоугольный участок (область интереса), который разбит на две области: область окна и область рамки (рис. 5). Предполагается, что сегментируемый объект полностью попадает внутрь окна, т. е. в рамке находится только фон (Ф), а в окне – как фон, так и объект (Об). Каждой точке (i, j) области интереса поставлен в соответствие вектор признаков Z T =(z1, z2 , …, zn).
Пусть нам известны априорные вероятности принадлежности точки в окне фону Р (Ф) или объекту Р (Об) = 1 – Р (Ф), величины штрафов за ошибочное отнесение точки объекта к фону С (Ф|Об) и точки фона к объекту С (Об|Ф). Тогда, как показано в литературе [2, 3], из условия минимума средних потерь при классификации точек в окне выводится следующее правило:
В лабораторной работе реализован частный случай байесовской сегментации - сегментация по правилу
Рис. 6. Пример сегментации по яркости тестового изображения
Рис. 7. Пример сегментации по яркости реального изображения
Вопрос о том, из каких признаков должен состоять вектор Z, чтобы получить хорошие результаты сегментации в самых разнообразных ситуациях, до сих пор не имеет однозначного ответа. На сегодняшний день широко используются яркостные, градиентные, спектральные и текстурные признаки. В работе выбраны два признака – яркость и норма ее градиента. К достоинствам байесовского подхода относится то, что он дает возможность использования многомерных гистограмм и позволяет правильно классифицировать объект при изменении его пространственной ориентации. Вместе с тем, требуется перебор многих параметров алгоритма, в том числе разрядности гистограмм признаков и размеров окна для достижения приемлемого результата. Подход на основе анализа гистограмм не учитывает локальной информации о положении точек изображения и их связности, что может не позволить ему эффективно отделить объект от неоднородного фона (рис. 7).
|


 Рис. 5. Рамка и окно на изображении
Рис. 5. Рамка и окно на изображении (18)
(18)
 где
где  ,
, 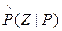 – многомерные гистограммы признаков Z, построенные в окне и в рамке соответственно, A = [(C (Об | Ф) + С (Ф | Об))/ C (Ф | Об)] – параметр стоимости неправильной классификации. При увеличении значения параметра А уменьшается число точек фона, ошибочно классифицированных как объект. Однако одновременно с этим увеличивается число точек объекта, принятых за точки фона, что может сильно исказить форму объекта. С другой стороны, если уменьшать величину параметра А, то многие точки фона будут классифицированы как объект.
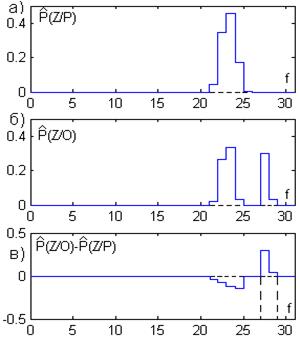
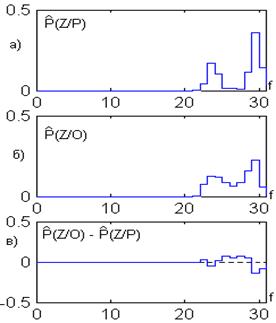
– многомерные гистограммы признаков Z, построенные в окне и в рамке соответственно, A = [(C (Об | Ф) + С (Ф | Об))/ C (Ф | Об)] – параметр стоимости неправильной классификации. При увеличении значения параметра А уменьшается число точек фона, ошибочно классифицированных как объект. Однако одновременно с этим увеличивается число точек объекта, принятых за точки фона, что может сильно исказить форму объекта. С другой стороны, если уменьшать величину параметра А, то многие точки фона будут классифицированы как объект. , что соответствует равенству штрафов С (Об|Ф) = С (Ф|Об) (А = 2) и равновероятной принадлежности точки в окне как фону, так и объекту Р (Ф) = Р (Об). На рис. 6 приведен пример сегментации только по яркости некоторого тестового изображения и гистограммы, поясняющих правило классификации. Точки, для которых выполняется условие
, что соответствует равенству штрафов С (Об|Ф) = С (Ф|Об) (А = 2) и равновероятной принадлежности точки в окне как фону, так и объекту Р (Ф) = Р (Об). На рис. 6 приведен пример сегментации только по яркости некоторого тестового изображения и гистограммы, поясняющих правило классификации. Точки, для которых выполняется условие  , считаются принадлежащими объекту, а остальные – фону. Результат классификации представляется в виде бинарной матрицы S (i, j), в которой единичные элементы соответствуют точкам объекта на исходном изображении, а нулевые – точкам фона. Для точной сегментации реальных изображений информации только от одного признака часто бывает недостаточно (рис. 7).
, считаются принадлежащими объекту, а остальные – фону. Результат классификации представляется в виде бинарной матрицы S (i, j), в которой единичные элементы соответствуют точкам объекта на исходном изображении, а нулевые – точкам фона. Для точной сегментации реальных изображений информации только от одного признака часто бывает недостаточно (рис. 7).