Теоретические сведения. Классический корреляционно–экстремальный алгоритм (КЭА) измерения координат объекта на изображении является частным случаем алгоритма поиска по критерию
Классический корреляционно–экстремальный алгоритм (КЭА) измерения координат объекта на изображении является частным случаем алгоритма поиска по критерию максимума апостериорной плотности в пространстве из двух параметров: координат центра объекта по горизонтальной и вертикальной осям [1,2]
где
Рис. 11 Координаты точек объекта в различных системах координат
Недостатками классического КЭА являются большое количество операций умножения, а также то, что он может давать грубые ошибки при наличии неоднородного фона на изображении. Если, например, яркость некоторых участков изображения окажется выше, чем яркость объекта, то взаимная корреляционная функция (21) даст неверный результат. Для уменьшения влияния колебаний яркости изображения на точность определения координат используют нормированную взаимную корреляционную функцию
Но ее вычисление потребует значительного большего объема вычислительных операций [2]. Для снижения требуемого объема вычислений было предложено использовать вместо корреляционных критериальных функций так называемые разностные критериальные функции [1,2]. Алгоритмы определения координат центра объекта, построенные на их основе, также относят к группе КЭА. Рассмотренный ранее классический корреляционный критерий можно отнести к критериям сходства двух изображений (эталонного и текущего). Существуют и другие критерии сходства (их можно найти в [1]), но их общим недостатком является необходимость перемножения элементов эталонного изображения (ЭИ) и текущего (ТИ), т. е. очень большой объем требуемых вычислений. В литературе все критерии сходства называют корреляционными функциями [1,2]. Разностные критериальные функции (следуя предложенной логике рассуждения) можно отнести к критериям отличия. Если критерии сходства требовалось максимизировать для нахождения координат центра объекта, то критерий отличия соответственно требуется минимизировать. По причине многоэкстремальности всех упомянутых критериев, порожденной неоднородным изображением фона, для отыскания глобального экстремума выбранного критерия целесообразно использовать метод полного перебора. Все многообразие разностных критериальных функций задается общей формулой
Преимуществом разностных критериальных функций перед корреляционными является отсутствие в них операции умножения. При использовании ЭВМ общего назначения это позволяет снизить вычислительные затраты в Наибольшее распространение получили критериальные разностные функции вида
Текущее изображение объекта с течением времени может изменяться из-за поворотов в пространстве, удаления, приближения, изменения освещенности и через некоторое время может стать совсем не похоже на эталонное изображение. В итоге может произойти потеря объекта. Поэтому необходимо своевременно учитывать все изменения в эталонном изображении объекта. При этом возникают вопросы, связанные с определением момента обновления эталонного изображения объекта и выбора способа его формирования. Самым простым способом обновления эталона является его смена после обработки каждого кадра и выбор в качестве нового эталона участка текущего кадра, взятого относительно найденных координат объекта. При этом предполагается, что изображение объекта вписывается с запасом, например в квадрат Экспериментальные исследования показали, что такой способ адаптации к возможным изменениям оказался неработоспособным из-за накопления погрешностей измерения координат, которые вызывают "случайные блуждания" объекта в эталоне и даже его уход из эталона. Это объясняется тем, что каждый акт определения координат путем вычисления экстремума той или иной критериальной функции сопровождается некоторой ошибкой, вызываемой эффектами пространственной дискретизации изображения, шумами, влиянием неравномерного фона. При многократной смене эталона очевидно неизбежное накопление ошибки и срыв слежения. Для борьбы с этим явлением было предложено несколько подходов. Один из них состоит в проверке целесообразности смены эталонного изображения путем сравнения глобального экстремума критериальной функции с некоторой пороговой величиной, например со значением критериальной функции, вычисленной в момент последней смены эталона. Это позволяет сократить число смен эталонного изображения, но принципиально не решает проблему накопления ошибки. Эффективным методом обновления эталонного изображения объекта является использование в качестве эталона усредненного изображения объекта. Усредненное изображение может быть получено с использованием алгоритма экспоненциального сглаживания
где С точки зрения требуемого объема вычислений более предпочтительным выглядит использование критерия (24), так как он не требует возведения в квадрат. Но при больших размерах зоны поиска необходимость отыскания глобального минимума критерия (24) может привести к неприемлемо большим вычислительным затратам. Необходимость использования КЭА в реальном масштабе времени заставляет искать возможность снизить требуемое количество вычислений без заметного ухудшения качества решения задачи слежения. Одним из возможных методов достижения этой цели является использование метода последовательных испытаний. Идея метода заключается в уменьшении количества вычислений в тех областях изображения, где искомый объект отсутствует. Эти области характеризуются быстрым ростом значения функции отличия с увеличением числа анализируемых точек. Считается, что объект отсутствует в анализируемой области изображения, если функция отличия растет быстрее, чем так называемая пороговая функция [2]. В данной работе реализован упрощённый метод последовательных испытаний. Это связано с особенностями реализации алгоритмов измерения координат в системе MATLAB. Суть этого метода состоит в следующем: вычисление критериальной разностной функции происходит несколько раз, причём сначала по участку, составляющему небольшую часть от эталона. Для этого участка выполняется проверка следующего условия:
где Если условие (27) выполняется, то алгоритм фиксирует отсутствие в данной области текущего кадра искомого объекта и переходит к рассмотрению следующей области. В противном случае алгоритм переходит на следующую ступень, увеличивая вчетверо площадь частичного участка эталона. Таким образом, изменяя коэффициент k и количество ступеней, можно добиться отсева большей части точек без потери устойчивости работы алгоритма.
|

 , (21)
, (21) - элементы наблюдаемого изображения
- элементы наблюдаемого изображения 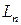 ;
;  - элементы дискретного эталонного изображения объекта;
- элементы дискретного эталонного изображения объекта; 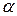 и
и 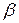 - координаты центра объекта в системе координат изображения Ln (рис. 11);
- координаты центра объекта в системе координат изображения Ln (рис. 11);  и
и  - координаты точек объекта в системе координат, связанной с центром объекта; n – номер кадра изображения.
- координаты точек объекта в системе координат, связанной с центром объекта; n – номер кадра изображения.
 . (22)
. (22)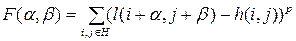 , где
, где  (23)
(23)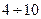 раз. В то же время, при малых отношениях сигнал - шум (менее трех) точностные характеристики разностных функций уступают корреляционным [1,2]. Под отношением сигнал – шум понимается отношение контраста объекта относительно фона к среднеквадратическому отклонению шума, присутствующего на изображении [2].
раз. В то же время, при малых отношениях сигнал - шум (менее трех) точностные характеристики разностных функций уступают корреляционным [1,2]. Под отношением сигнал – шум понимается отношение контраста объекта относительно фона к среднеквадратическому отклонению шума, присутствующего на изображении [2]. ; (24)
; (24)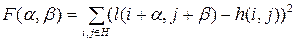 . (25)
. (25)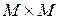 точек, причем центр объекта совпадает с центром квадрата. Очевидно, в эталонном изображении кроме объекта будут присутствовать точки окружающего фона.
точек, причем центр объекта совпадает с центром квадрата. Очевидно, в эталонном изображении кроме объекта будут присутствовать точки окружающего фона. , (26)
, (26)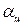 ,
, 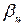 - координаты центра объекта, найденные в n -м кадре; b - параметр экспоненциального сглаживания, выбираемый в диапазоне от 0 до 1. При b =1 эталонное изображение не обновляется, при b =0 осуществляется покадровая смена эталона, а при 0 <b<;1 эталонное изображение формируется путем межкадрового усреднения изображения объекта. Достоинством такого подхода является малая чувствительность к ошибкам дискретизации, в отличие от алгоритмов с покадровой сменой эталона. Кроме этого, использование межкадровой фильтрации позволяет повысить точность за счет подавления шумов, присутствующих на изображении.
- координаты центра объекта, найденные в n -м кадре; b - параметр экспоненциального сглаживания, выбираемый в диапазоне от 0 до 1. При b =1 эталонное изображение не обновляется, при b =0 осуществляется покадровая смена эталона, а при 0 <b<;1 эталонное изображение формируется путем межкадрового усреднения изображения объекта. Достоинством такого подхода является малая чувствительность к ошибкам дискретизации, в отличие от алгоритмов с покадровой сменой эталона. Кроме этого, использование межкадровой фильтрации позволяет повысить точность за счет подавления шумов, присутствующих на изображении.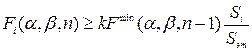 , (27)
, (27)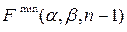 – минимум критериальной функции, вычисленный в предыдущем (n – 1) кадре;
– минимум критериальной функции, вычисленный в предыдущем (n – 1) кадре; 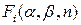 – критериальная функция, вычисленная по частичному участку эталона на i -й ступени алгоритма в n –ом кадре; k – весовой коэффициент;
– критериальная функция, вычисленная по частичному участку эталона на i -й ступени алгоритма в n –ом кадре; k – весовой коэффициент;  – площадь (количество точек) всего эталона;
– площадь (количество точек) всего эталона;  - площадь частичного участка эталона.
- площадь частичного участка эталона.


