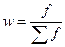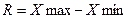СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ И ИХ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
ЛЕКЦИЯ 5 Составной частью сводной обработки данных статистического наблюдения является построение рядов распределения. Цель его - выявление основных свойств и закономерностей исследуемой статистической совокупности.
Представленные выше данные без какой-либо систематизации образуют так называемый первичный ряд данных. Первым шагом в упорядочении первичного ряда является его ранжирование, т.е. расположение всех вариантов ряда в возрастающем (или убывающем) порядке. Число повторений отдельных вариантов значений признаков называют частотой повторения. В дальнейшем частоту повторения значения признака будем обозначать По характеру вариации различают дискретные и непрерывные признаки. Дискретные признаки отличаются друг от друга на некоторую конечную величину, т.е. даны в виде прерывных чисел. Непрерывные признаки могут отличаться один от другого на сколь угодно малую величину и в определенных границах принимать любые значения. Способы построения вариационного ряда для этих видов признаков различны. Для построения дискретного ряда с небольшим числом вариантов достаточно перечислить все встречающиеся варианты значений признака, обозначаемые через х,а затем подсчитать частоту повторения каждого варианта
В тех случаях, когда число вариантов дискретного признака достаточно велико, а также при анализе вариации непрерывного признака, когда значения признака у отдельных единиц могут вообще не повторяться, строятся интервальные ряды распределения. При построении интервальных рядов распределения необходимо прежде всего установить число групп (интервалов), на которые следует разбить все единицы изучаемой совокупности. Определение величины интервала i для построения вариационного ряда с равными интервалами производится следующим образом: 1) вычисляется разность между максимальным и минимальным значениями признака первичного ряда (определяется размах вариации, R):
2) размах вариации делится на число групп к, т.е. Число групп приближенно определяется по формуле Стерджесса: k = 1+3,322 lg n, где n- общее число изучаемых единиц совокупности. Указанное выражение почти всегда оказывается дробной величиной, которую округляют до целого числа, поскольку количество групп не может быть дробным. Рассмотрим построение ряда распределения по первичным данным о размере прибыли 20 коммерческих банков за год (млрд руб.): 3,7; 4,3; 6,7; 5,6; 5,1; 8,1; 4,6; 5,7; 6,4; 5,9; 5,2; 6,2; 6,3; 7,2; 7,9; 5,8; 4,9; 7,6; 7,0; 6,9. Определяем количество групп интервального вариационного ряда: к= 1+3,3221g20= 1+3,322*1,301= 5,32. Округляя, получим число групп, равное 5. Величина интервала составит 0,9 млрд руб.
|


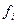 а сумму частот, равную объему изучаемой совокупности
а сумму частот, равную объему изучаемой совокупности  или
или 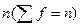 , где n - число вариантов значений признака.
, где n - число вариантов значений признака.