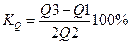Показатели центра распределения
Средняя арифметическая для дискретного ряда распределения рассчитывается по формуле
x- варианты значений признака f- частота повторений данного варианта
В интервальном вариационном ряду средняя арифметическая определяется по формуле
где В отличие от средней арифметической, рассчитываемой на основе использования всех вариантов значений признака, мода и медиана характеризуют величину варианта, занимающего определенное положение в ранжированном вариационном ряду. Медиана (Ме) соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы определяется ее номером В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Для определения их величины используются следующие формулы:
где
Мода (Мо) - наиболее часто встречающееся значение признака в совокупности - для данного ряда распределения также равна четвертому разряду (этому разряду соответствует максимальная частота, равная 8). Наибольшая частота соответствует также интервалу 5,5 - 6,4, т.е. мода должна находиться в этом интервале. Ее величину определяем по формуле:
где
Показатели вариации (колеблемости) признака Размах колебаний, или размах вариации, представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности:
Среднее линейное отклонение а вычисляется по следующим формулам: для несгруппированных данных для сгруппированных данных Дисперсия для несгруппированных данных: для сгруппированных данных
Среднее квадратическое отклонение для несгруппированных данных для сгруппированных данных Размах вариации, среднее линейное и среднее квадратическое отклонение являются величинами именованными. Они имеют те же единицы измерения, что и индивидуальные значения признака.
Расчет показателей вариации для банков, сгруппированных по размеру прибыли, показан в Таблице
Если в качестве показателя центра распределения используется медиана, то для характеристики вариации признаков в совокупности можно применить так называемое квартильное отклонение
где Q1 и Q3—соответственно первая и третья квартили распределения Квартили определяются по формулам, аналогичным приведенной выше формуле для расчета медианы. При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации. Эти показатели вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане). Коэффициент осцилляции: Относительное линейное отклонение Коэффициент вариации Относительный показатель квартильной вариации
Наиболее часто применяемый показатель относительной колеблемости - коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
|



 - середина соответствующего интервала.
- середина соответствующего интервала.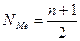 , где n-число единиц в совокупности.
, где n-число единиц в совокупности.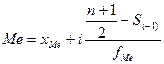
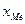 нижняя граница медианного интервала;
нижняя граница медианного интервала; - величина интервала;
- величина интервала;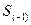 - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному; - частота медианного интервала.
- частота медианного интервала.
 - начало модального интервала;
- начало модального интервала;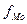 - частота, соответствующая модальному интервалу;
- частота, соответствующая модальному интервалу; предмодальная частота;
предмодальная частота; - послемодальная частота.
- послемодальная частота.
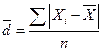

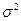 - средняя из квадратов отклонений вариантов значений признака от их средней величины. Дисперсия рассчитывается по следующим формулам:
- средняя из квадратов отклонений вариантов значений признака от их средней величины. Дисперсия рассчитывается по следующим формулам:

 представляет собой корень квадратный из дисперсии:
представляет собой корень квадратный из дисперсии:
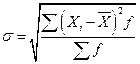
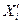
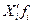


 млрд руб
млрд руб млрд руб.
млрд руб.
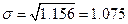 млрд руб.
млрд руб.
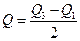

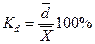

 , или
, или