Организация циклов в программе. Рекуррентной называется формула, связывающая значения р+1 соседних членов uk, uk-1, , uk-p (k>=p+1) некоторой последовательности {un}(n=1

 

Рекуррентной называется формула, связывающая значения р+1 соседних членов uk, uk-1, …, uk-p (k>=p+1) некоторой последовательности {un}(n=1, 2, …): uk=F(k, uk-1, …, uk-p). Рекуррентная формула позволяет шаг за шагом определить любой член последовательности, если известны р первых её членов u1, u2, …, up, где р называют порядком формулы.

Рассмотрим задачу нахождения n-го члена рекуррентной последовательности на примере чисел Фибоначчи. Каждое число Фибоначчи равно сумме двух предыдущих. В частности:

U3 = u2+u1 = 1+1 = 2;

U4 = u3+u2 = 1+2 = 3 и т.д.

Отсюда следует, что для получения очередного числа достаточно хранить два предыдущих. Таким образом, в программе постоянно используются три соседних числа Фибоначчи. Для их хранения достаточно ввести три переменных: А хранит uk, B хранит uk-1, С хранит uk-2. Для вычисления следующего числа Фибоначчи необходимо провести сдвиг, т.е. переписать содержимое В в С, а содержимое А в В. Исходя из этого, получим фрагмент

{фрагмент}

c=1 ‘значение первого числа известно

b=1 ‘значение второго числа тоже известно

k=3 ‘начинаем вычисление с третьего числа

while k<=n ‘цикл, пока не найдено n-е число

a=b+c ‘вычисляем следующее число как сумму двух предыдущих

c=b ‘сдвигаем b в c для нахождения следующего числа

b=a ‘сдвигаем a в b для нахождения следующего числа

k=k+1 ‘увеличиваем счетчик найденных чисел

wend

Print a ‘выводим найденное число

Цель задания:

1. Получение навыков в выборе и использовании

операторов цикла.

2. Знакомство с итерационными процессами.

Постановка задачи:

Используя, оператор цикла, найти сумму элементов, указанных в конкретном варианте. Результат напечатать, снабдив соответствующим заголовком.

Содержание отчета:

1. Постановка задачи.

2. Текст программы.

3. Результат решения конкретного варианта.

Методические указания:

При определении суммы членов ряда следует использовать рекуррентную формулу для получения следующего члена ряда.

Факториалом целого числа называют произведение

1*2*3*…*n = n!

n! = n*(n-1)

Например, требуется найти сумму ряда с точностью e=10^-4, общий член которого .

Для получения рекуррентной формулы вычислим отношение:

,

откуда:

.

При составлении программы считать, что точность достигнута, если а_n <e
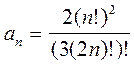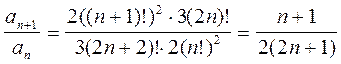