Теорема. Пусть дана система дифференциальных уравнений
где (1) если (2) если Теорема не даёт ответа на вопрос об устойчивости решений в случае, когда Нелинейные системы часто удаётся исследовать на устойчивость, осуществив линеаризацию системы, т.е. замену нелинейной на близкую к ней (в определённом смысле) линейную систему. А именно, пусть система имеет вид
Выделим каким-либо способом у функций
где
|
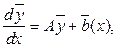
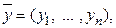
матрица размера 
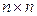с элементами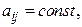 
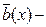непрерывная вектор-функция, определённая для 
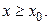Пусть 
– собственные значения матрицы А. Тогда:
то всякое решение системы устойчиво;
для какого-либо 
то всякое решение системы неустойчиво.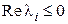
при всех 
и 
для какого-либо 
(
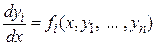главную линейную часть (т.е. разложим функции 
достаточно мала. Тогда вопрос об устойчивости нелинейной системы сведётся к аналогичному вопросу для линейной системы с постоянными коэффициентами, а он рассматривался в предыдущей теореме. Точный математический смысл высказанного утверждения даётся следующей теоремой, доказательство которой здесь не приводится и может быть найдено в учебниках по дифференциальным уравнениям с более подробным изложением.
