Понятие о законе больших чисел и предельных теоремах
Закон больших чисел. Под законом больших чисел (ЗБЧ) в широком смысле понимается общий принцип, согласно которому по формулировке академика А.Н.Колмогорова, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестаёт быть случайным и может быть предсказан с большой степенью определённости. Под ЗБЧ в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определённым постоянным. Исторически первой формулировкой ЗБЧ была теорема Бернулли. Теорема Бернулли. Относительная частота события в n повторных независимых испытаниях, в каждом из которых оно может появиться с одной и той же вероятностью р, при неограниченном увеличении числа n сходится по вероятности к вероятности р этого события в отдельном испытании:
Смысл теоремы Бернулли состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что относительная частота (или статистическая вероятность) события Теорема Бернулли связывает формальное аксиоматическое определение вероятности с эмпирическим (опытным) законом постоянства относительной частоты, тем самым она даёт возможность обосновать широкое применение на практике вероятностных методов исследования. Наиболее важной формой закона больших чисел является теорема Чебышева, следствием которой является теорема Бернулли. Теорема Чебышева. Если независимые случайные величины
Центральная предельная теорема. Очень часто значение, которое принимает исследуемая случайная величина Y, является результатом суммарного воздействия ряда случайных факторов
|

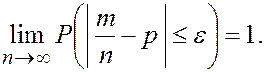 (11.33)
(11.33)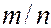 – величина случайная, как угодно мало отличается от неслучайной величины р – вероятности события, т.е. перестаёт быть случайной. Поэтому теорема Бернулли даёт теоретическое обоснование замены неизвестной вероятности события его относительной частотой, или статистической вероятностью, полученной в n повторных независимых испытаний, проводимых при одном и том же комплексе условий.
– величина случайная, как угодно мало отличается от неслучайной величины р – вероятности события, т.е. перестаёт быть случайной. Поэтому теорема Бернулли даёт теоретическое обоснование замены неизвестной вероятности события его относительной частотой, или статистической вероятностью, полученной в n повторных независимых испытаний, проводимых при одном и том же комплексе условий.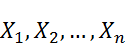 имеют одинаковое математическое ожидание, равное а, а их дисперсии ограничены одной и той же константой, то при неограниченном возрастании числа n средняя арифметическая случайных величин сходится по вероятности к математическому ожиданию а случайных величин:
имеют одинаковое математическое ожидание, равное а, а их дисперсии ограничены одной и той же константой, то при неограниченном возрастании числа n средняя арифметическая случайных величин сходится по вероятности к математическому ожиданию а случайных величин: (11.34)
(11.34) . Если эти факторы слабо зависят друг от друга и ни один из них не является доминирующим, то их сумма имеет распределение, близкое к нормальному. Такая ситуация наиболее характерна для процессов измерения. Дело в том, что результат измерения складывается под влиянием многочисленных независимых причин, причём влияние каждой из них на суммарный результат незначительно. Например, на величину температуры в конкретном месте в комнаты оказывает влияние близость отопительных приборов, наличие и расположение в комнате людей, потоки воздуха, влажность, температура воздуха на улице, наличие источников света и их мощность, расположение окон, дверей и т.д.
. Если эти факторы слабо зависят друг от друга и ни один из них не является доминирующим, то их сумма имеет распределение, близкое к нормальному. Такая ситуация наиболее характерна для процессов измерения. Дело в том, что результат измерения складывается под влиянием многочисленных независимых причин, причём влияние каждой из них на суммарный результат незначительно. Например, на величину температуры в конкретном месте в комнаты оказывает влияние близость отопительных приборов, наличие и расположение в комнате людей, потоки воздуха, влажность, температура воздуха на улице, наличие источников света и их мощность, расположение окон, дверей и т.д.


