Линейные функции от случайных величин
1. Если а) сл. в. б) 2. Если 3. Дана система независимых случайных величин
В частности, если все значения
будет случайной величиной, распределенной по нормальному закону с математическим ожиданием, совпадающим с математическим ожиданием для одного измерения и среднеквадратичным отклонением
На практике для получения закона распределения, который приближенно может быть принят за нормальный, обычно оказывается достаточным наличие 5-10 слагаемых в выражении (3.22). Следует заметить, что это не относится к случаю, когда дисперсия одного из слагаемых в этой формуле подавляюще велика по сравнению со всеми другими; предполагается, что случайные слагаемые в сумме (3.22) по своему рассеиванию имеют примерно один и тот же порядок. Если эти условия соблюдены, то для величины может быть приближенно принят нормальный закон с параметрами, определяемыми формулами
Распределение вероятностей произведения двух независимых случайных величин X и Y, распределенных по нормальному закону, в отличие от суммы, уже не будет распределено по нормальному закону. В общем случае распределение оказывается достаточно громоздким. Пример 3.16. Производится измерение без систематических ошибок диаметра вала. Случайная ошибка измерения X подчиняется нормальному закону распределения со средним квадратическим отклонением 20мм. Найти: а) вероятность того, что измерение будет произведено с ошибкой, по абсолютной величине не превосходящей 35 мм; б) интервал, в который попадет сл.в. X с вероятностью 0,6827. Решение. Ошибка измерения а) По формуле 3.20 б) Пример 3.17. Сл. в. Решение. Так как нормальная кривая
симметрична относительно кривой
Поскольку эти площади численно равны вероятностям попадания
Пример 3.18. Полагая, что рост мужчин определённой возрастной группы есть нормально распределённая случайная величина 1. а) выражение плотности вероятности и функции распределения случайной величины 2. квантиль x0,7 и объяснить смысл полученного значения. 3. Сформулировать правило «трёх сигм» для случайной величины Решение.1. а) По формулам (3.17) и (3.19) запишем плотность распределения и функцию распределения:
б) Доля костюмов 4-го сорта в общем объёме производства определяется по формуле (3.16) как вероятность попадания сл.в. X в заданный интервал:
Здесь Таким образом, для данной возрастной группы в общем объёме производства нужно предусмотреть примерно 24% костюмов. 2. По таблице III приложений найдём
Это означает, что 70% мужчин данной возрастной группы имеют рост до 176 см. 3. Практически достоверно, что рост мужчин данной возрастной группы заключён в границах от Пример 3.19. Значения случайной величины X с вероятностью 0,9973 попадают в интервал Решение. Таким свойством обладает нормально распределённая случайная величина, поэтому В силу особенностей нормального закона распределения, отмеченных в начале параграфа, он занимает центральное место в теории и практике вероятностно-статистических методов. 3.17. Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина), равной 50 мм. Фактическая длина изготовленных деталей не менее 32 мм и не более 68 мм. Деталь считается годной, если отклонение её длины от проектной не превышает s. Сколько процентов годных деталей штампует автомат? 3.18. Случайная величина X распределена нормально с параметрами 3.19. Значения случайной величины X с вероятностью 0,9545 попадают в интервал (2;10). Найдите математическое ожидание и дисперсию этой случайной величины.
|

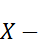 нормальная случайная величина с параметрами
нормальная случайная величина с параметрами  и
и 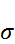 , а
, а  постоянная, то:
постоянная, то: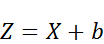 распределена по нормальному закону с параметрами
распределена по нормальному закону с параметрами  и
и 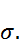
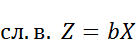 распределена по нормальному закону с параметрами
распределена по нормальному закону с параметрами 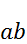 и
и  .
. и
и 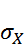 ,
, 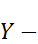 нормальная сл.в. с параметрами
нормальная сл.в. с параметрами 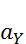 и
и 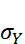 , то сл.в.
, то сл.в. 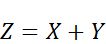 распределена по нормальному закону с
распределена по нормальному закону с 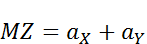 и
и 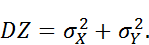
 с математическими ожиданиями
с математическими ожиданиями  и дисперсиями
и дисперсиями 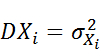 . Рассмотрим сл.в.
. Рассмотрим сл.в.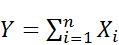 . (3.22)
. (3.22)
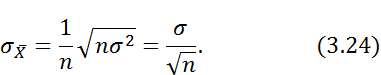
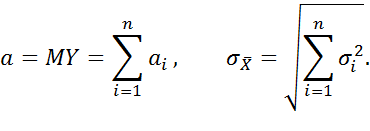
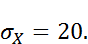 Так как по условию систематическая ошибка отсутствует, то
Так как по условию систематическая ошибка отсутствует, то 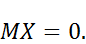


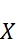 распределена нормально с математическим ожиданием
распределена нормально с математическим ожиданием 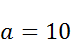 . Вероятность попадания
. Вероятность попадания 
 то площади, ограниченные сверху нормальной кривой и снизу – интервалами (0;10) и (10;20), равны между собой.
то площади, ограниченные сверху нормальной кривой и снизу – интервалами (0;10) и (10;20), равны между собой.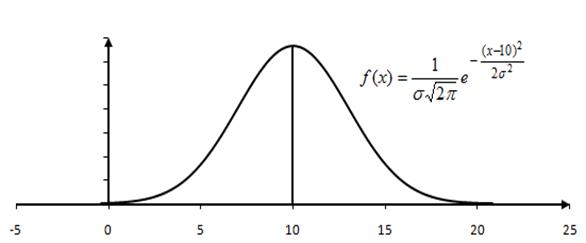
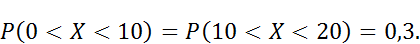
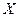 с параметрами
с параметрами 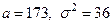 , найти:
, найти: ,
,  .
.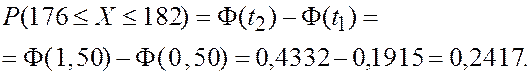
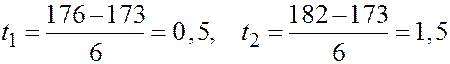 .
. .
. и
и
 .
. до
до  , т.е.
, т.е. 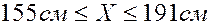 .
.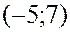 . Найдите математическое ожидание и дисперсию этой случайной величины.
. Найдите математическое ожидание и дисперсию этой случайной величины. ,
,  ,
, 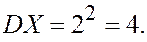
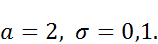 Найти интервал, в котором с вероятностью 0,9973 будут заключены значения сл.в. X.
Найти интервал, в котором с вероятностью 0,9973 будут заключены значения сл.в. X.


