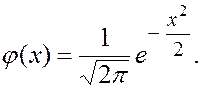Нормальный закон распределенияНормальный закон распределения наиболее часто встречается на практике. Главная его особенность состоит в том, что он является предельным законом, к которому приближаются другие законы при весьма часто встречающихся типичных условиях. Определение: Непрерывная случайная величина
где Нормальное распределение симметрично:
Наиболее вероятное значение величины
Рисунок 1. График функции распределения нормального закона с параметрами
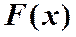
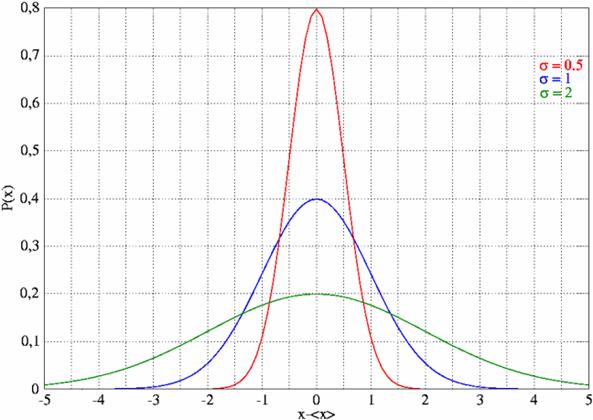
Рисунок 2 Нормальное распределение с параметрами
|
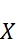имеет нормальный закон распределения (закон Гаусса) с параметрами 
и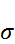 
, если плотность распределения имеет вид
(3.17)
.
, 
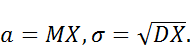
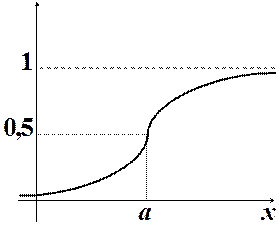
называется стандартным нормальным распределением. Его плотность задается функцией Гаусса
