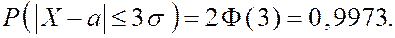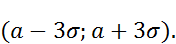Свойства нормального распределения
1. Вероятность попадания нормальной случайной величины в интервал
где
2. Вероятность того, что отклонение нормальной случайной величины от своего математического ожидания
Найдем вероятности отклонения нормальной случайной величины от математического ожидания на величину
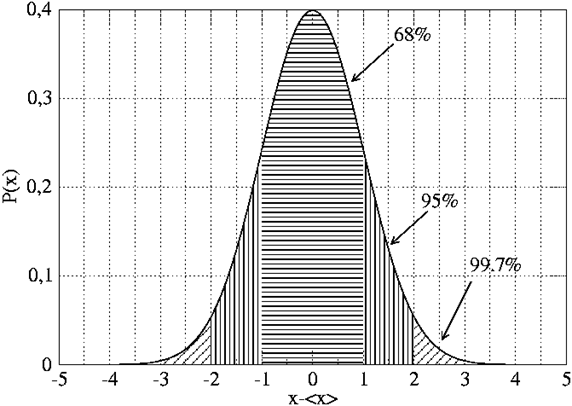
Отсюда вытекает «Правило трех сигм»: С вероятностью, практически равной единице, значения нормальной случайной величины попадают в интервал
Рисунок 2.
|
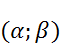равна
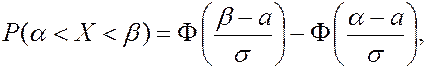(3.18)
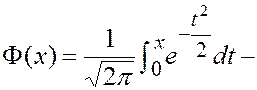функция Лапласа, ее значения приведены в таблице III приложений. Так как 
, то функция распределения случайной величины 
распределённой по нормальному закону, определяется формулой: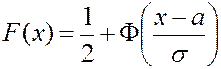
. (3.19)
не превысит величину 
(по абсолютной величине), равна
(3.20)
Значения функции Лапласа находим в приложении.
(3.21)
