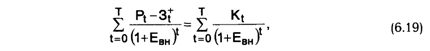Чистый дисконтированный доход
Чистый дисконтированный доход (ЧДД,) определяется как сумма текущих эффектов за весь расчетный период, приведенная к начальному шагу, или как превышение интегральных результатов над интегральными затратами. Если в течение расчетного периода не происходит инфляционного изменения цен или расчет производится в базовых ценах, то величина ЧДД для постоянной нормы дисконта вычисляется по формуле
где Pt — результаты, достигаемые на t-ом шаге расчета; Зt — затраты, осуществляемые на том же шаге; Т — горизонт расчета (равный номеру шага расчета, на котором производится ликвидация объекта"). Эt = (Pt —Зt) — эффект, достигаемый на t-ом шаге. Если ЧДД инвестиционного проекта положителен, проект является эффективным (при данной норме дисконта) и может рассматриваться вопрос о его принятии. Чем больше ЧДД, тем эффективнее проект. Если инвестиционный проект будет осуществлен при отрицательном ЧДД, инвестор понесет убытки, т.е. проект неэффективен. На практике часто пользуются модифицированной формулой для определения ЧДД. Для этого из состава Зt исключают капитальные вложения и обозначают через: Kt — капиталовложения на t-ом шаге; К — сумму дисконтированных капиталовложений, т.е.
* В формулу для К убыток входит со знаком "плюс", а доход — со знаком "минус";.
Тогда формула (6.15) для ЧДД записывается в виде
и выражает разницу между суммой приведенных эффектов и приведенной к тому же моменту времени величиной капитальных вложений (К). Индекс доходности (ИД) представляет собой отношение суммы приведенных эффектов к величине капиталовложений
Индекс доходности тесно связан с ЧДД. Он строится из тех же элементов и его значение связано со значением ЧДД: если ЧДД положителен, то ИД >1 и наоборот. Если ИД >1, проект эффективен, если ИД < 1 — неэффективен. Внутренняя норма доходности (ВНД)* представляет собой ту норму дисконта (Евн), при которой величина приведенных эффектов равна приведенным капиталовложениям.
* При использовании ВНД следует соблюдать известную осторожность. Во-первых, она не всегда существует. Во-вторых, уравнение (6.19) может иметь больше одного решения. Первый случай весьма редок. Во втором корректный расчет ВНД несколько затруднителен, хотя и возможен. В качестве первого приближения в ситуации, когда простой (недисконтированный) интегральный эффект положителен, ряд авторов предлагает принимать в качестве Евн значение наименьшего положительного корня уравнения (6.19).
Иными словами, Евн (ВНД) является решением уравнения
Если расчет ЧДД инвестиционного проекта дает ответ на вопрос, является он эффективным или нет при некоторой заданной норме дисконта (Е), то ВНД проекта определяется в процессе расчета и затем сравнивается с требуемой инвестором нормой дохода на вкладываемый капитал. В случае, когда ВНД равна или больше требуемой инвестором нормы дохода на капитал, инвестиции в данный инвестиционный проект оправданы, и может рассматриваться вопрос о его принятии. В противном случае инвестиции в данный проект нецелесообразны (см. приложение 5 к Рекомендациям). Если сравнение альтернативных (взаимоисключающих) инвестиционных проектов (вариантов проекта) по ЧДД и ВНД приводят к противоположным результатам, предпочтение следует отдавать ЧДД (подробнее см. приложение 5 к Рекомендациям).
|

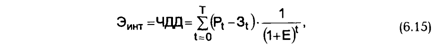
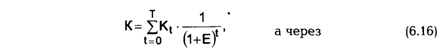
 — затраты на t-ом шаге при условии, что в них не входят капиталовложения.
— затраты на t-ом шаге при условии, что в них не входят капиталовложения.