Деформування і руйнування гірських порід
При бурінні свердловин мають місце виключно динамічні процеси. Якщо для опису статичних процесів достатня система рівнянь рівноваги сил і моментів, то для динамічних процесів додатково потрібно мати рівняння балансу енергії. Динамічні процеси є складнішими і не можуть бути вивченими в статичних умовах. З точки зору буріння слід вивчати динамічне прикладення навантаження з боку елементів озброєння долота до гірської породи. При цьому слід мати на увазі, що ці процеси призводять до пластичного деформування і крихкого руйнування породи. Вони не піддаються єдиному математичному описові, і при їх вивченні основну роль відіграють експериментальні дослідження. При експериментальному вивченні динамічного деформування і руйнування порід застосовуються принципи наближеного моделювання, котрі реалізуються на спеціальних установках. Найширше використовуються установки двох типів: копрові і кулачкові. На копрових установках використовується удар вільно падаючого ударника, або ударника, який розганяється прикладеною силою, наприклад тиском повітря. На кулачкових установках задається закон руху породруйнуючого елемента відносно породи, що дає змогу повніше моделювати процес його взаємодії з породою. Строгий математичний опис процесу взаємодії породоруйнуючих елементів з гірською породою можна дати лише для найпростіших випадків. Перший випадок. По поверхні породи, яка є пружним півпростором, здійснюється удар жорстким ударником масою m, який вільно падає. На момент контакту швидкість руху ударника v=v0, а прикладена до нього сила Р дорівнює нулю в процесі усього деформування (рис 11.1). Кінетична енергія вантажу, що падає, на початок контактування з пружним тілом
де К – коефіцієнт пропорційності, який залежить від пружних властивостей гірської породи і форми робочої поверхні ударника. Максимальною сила взаємодії буде при максимальному зміщенні поверхні (d0), тобто в момент, коли швидкість руху ударника зменшиться до нуля. При цьому потенціальна енергія деформування складе
або з урахуванням виразу (11.2)
З умови U = Uк можна визначити максимальне зміщення поверхні
і далі найбільшу силу взаємодії
Другий випадок. Розглянемо ту ж задачу при P=const. Тоді баланс енергії при d=d0 запишеться в вигляді
Розв’язок рівняння (11.7) має вигляд
Враховуючи фізичний смисл процесу, приймаємо знак плюс. Підставивши значення d0 у вираз (11.2), визначимо максимальну силу взаємодії
Якщо v0=0, то Fma x= 2P, тобто має місце так звана несподівана взаємодія (миттєве прикладення навантаження).
|

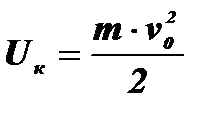 (11.1)
(11.1) Рисунок 11.1 − Розрахункова схема для вивчення взаємодії ударника з породою
Рисунок 11.1 − Розрахункова схема для вивчення взаємодії ударника з породою
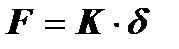 , (11.2)
, (11.2) , (11.3)
, (11.3) . (11.4)
. (11.4) , (11.5)
, (11.5)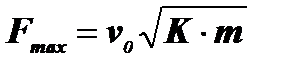 . (11.6)
. (11.6) (11.7)
(11.7)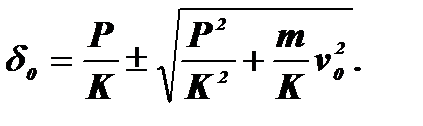 (11.8)
(11.8) (11.9)
(11.9)


