Числа подобия при моделировании обтекания автомобиля
Получим числа подобия, предполагая, что объект и модель удовлетворяют второму закону Ньютона
Запишем этот закон для реального объекта
из которых найдем переменные для модели
подставим их в уравнение для модели
Из тождественности уравнений для объекта и модели вытекает
Выражение
называется условием подобия. Равенство (6.61) представляет собой математическое выражение первой теоремы подобия, которая гласит: у подобных явлений индикаторы подобия равны единице. Смысл равенства единице индикатора подобия заключается в том, что существенное значение для динамического подобия процессов имеет не каждый из параметров, входящих в закон Ньютона в отдельности (F, m, t, x), а вполне определенная их комбинация, называемая числом Ньютона
Число Ньютона называется инвариантом подобия и характеризует отношение изменения импульса силы (Ft) к импульсу (mv, v = l/t), оно одинаково для всех подобных между собой явлений, и первая теорема подобия может быть сформулирована так: у подобных явлений числа подобия (K) принимают одно и то же значение, т.е. эти явления тождественны
Слово idem применяется для обозначения подобных процессов. Для обобщения условия динамического подобия рассмотрим более сложный вариант, вытекающий из второго закона Ньютона – одномерное стационарное течение вязкого воздуха, обтекающего автомобиль, движущийся со скоростью vx в направлении оси x. При этом скорость частиц воздуха вблизи поверхности автомобиля, у которой реализуются силы трения, зависит от двух координат x и y. Соответствующее уравнение Навье-Стокса, описывающее стационарный перенос импульса под действием сил тяжести, внешнего давления и вязкого трения, является частным случаем уравнения (6.11) и имеет вид:
Для записи этого уравнения в безразмерном виде выберем в качестве масштабов следующие характерные величины: l – характерный размер области; р 0 – давление; v 0 – скорость. Тогда безразмерные переменные (они обозначены сверху чертой) примут вид
Отсюда получаются размерные переменные Подставим эти размерные переменные в уравнение Навье-Стокса (6.64) и вынесем постоянные масштабы за знаки частных производных
после умножения уравнения на
Уравнение (7.65) безразмерно, следовательно, каждый из трех комплексов в правой части уравнения безразмерен и является инвариантом подобия
где Fr, Eu, Re – соответственно числа Фруда, Эйлера и Рейнольдса. Числа подобия можно получить непосредственно из уравнения переноса импульса для вязкой среды (6.64), анализируя размерность. Действительно, уравнение
представляет баланс сил инерции (1), тяжести (2), внешнего давления (3) и вязкого трения (4). Отношение первого члена уравнения, характеризующего силы инерции при стационарном течении, к четвертому, характеризующему силы вязкого трения, является важнейшим критерием подобия, называемым числом Рейнольдса
При малых значениях числа Рейнольдса ( Область изменения числа Рейнольдса Таким образом, число Рейнольдса, характеризующее отношение сил инерции к силам вязкого трения, играет важную роль для определения структуры течения воздуха, обтекающего транспортное средство при движении. Отношение второго члена уравнения (4.12) к первому дает число Фруда
характеризующее относительную по сравнению с инерционной силу тяжести. Из сравнения сил внешнего давления с силами инерции в уравнении (6.67)
получается число Эйлера Числа Фруда и Рейнольдса определяют геометрию и физические свойства системы и являются ее параметрами, т.к. могут измениться при переходе к другой системе. Эти числа подобия называются определяющими. Число Эйлера характеризует безразмерный перепад давления, который подлежит определению и называется определяемым числом. С учетом чисел подобия уравнение Навье-Стокса (6.64) принимает вид:
Первая теорема подобия требует тождественности чисел подобия как необходимого условия подобия явлений. Особый интерес представляют соотношения между числами подобия. Возможность представления решения как функции от чисел подобия в виде критериального уравнения и составляет содержание второй теоремы подобия (π-теоремы): любое уравнение, связывающее между собой N физических величин, из которых K величин обладают независимыми размерностями, можно преобразовать к уравнению, связывающему N–K безразмерных критериев Смысл этой теоремы рассмотрим на примере уравнения Навье-Стокса (6.64), решение которого при соответствующих краевых условиях должно иметь следующий вид
Искомые величины – скорость и давление являются функциями двух аргументов (координат x и y) и пяти параметров (плотности ρ, динамической вязкости η, ускорения свободного падения g, масштабов скорости v 0 и длины l). После приведения уравнения к безразмерному виду (6.68) имеем решение
при этом каждая искомая величина зависит уже от двух безразмерных координат и двух параметров. В рассматриваемой задаче число параметров при переходе к безразмерным переменным уменьшилось на три. В решении (6.70) числа подобия, составленные из параметров (Fr, Re), называются определяющими, а безразмерная скорость Условия, достаточные для существования подобия физических явлений (третья теорема подобия), были впервые сформулированы в 1930 году Кирпичевым и Гухманом в виде трех положений: 1) подобные процессы должны быть качественно одинаковыми, т.е. они должны иметь одинаковую физическую природу и описываться одинаковыми дифференциальными уравнениями; 2) условия однозначности (геометрические и физические параметры системы, начальные и граничные условия) подобных процессов должны быть одинаковыми во всем, кроме численных значений размерных постоянных, содержащихся в этих условиях; 3) одноименные определяющие критерии подобных процессов должны иметь одинаковые численные значения. Отметим следствия теоремы: 1) если процессы А и В подобны, то любая физическая величина φ в данной точке процесса А пропорциональна соответствующей величине в сходственной точке процесса В; 2) подобные процессы можно рассматривать как один и тот же процесс, но взятый в различном масштабе, причем масштабы разноименных величин могут быть неодинаковыми.
Пример 6.3. При моделировании испытаний автомобиля в аэродинамической трубе изготовлена модель автомобиля, уменьшенная в 10 раз (рис. 6.5). Критерием, определяющим режим обтекания автомобиля воздухом, является число Рейнольдса 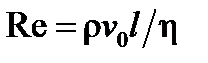 . .
Первое условие теоремы Кирпичева-Гухмана выполнено, т.к. в модели и в реальных условиях одна и та же моделирующая среда – воздух. Второе условие (однородность профиля скорости потока воздуха) выполняется не во всем объеме аэродинамической трубы, а только в её рабочей части за пределами гидродинамических пограничных слоёв толщиной δ, в пределах которых профиль скорости изменяется. Третье условие – равенство чисел Рейнольдса – выполняется, если в модели увеличить скорость в 10 раз или уменьшить вязкость воздуха в 10 раз. Последнее нереально. Значительное увеличение скорости может привести к ионизации воздуха, появлению ударных волн (при достижении скорости звука) при этом изменяется дифференциальное уравнение течения ионизированного воздуха и нарушается первое условие. Поэтому работа с моделью автомобиля, уменьшенной в 10 раз, не отвечает условиям подобия. В аэродинамических трубах продувают автомобили натуральных размеров. Функциональные зависимости определяемых критериев от критериев определяющих (6.70) описывают все подобные явления. Однако определяющие критерии, характеризующие соотношение определенных физических факторов, могут принимать очень большие или очень малые значения и перестают оказывать влияние на протекание процесса. Это явление называется вырождением критерия или автомодельностью процесса по отношению к данному критерию. Смысл термина заключается в том, что при изменении вырожденного критерия безразмерные характеристики процесса не изменяются, т.е. он остается подобным самому себе, моделирует сам себя. Например, в уравнениях (6.68) при течении вязкого газа влияние силы тяжести может быть пренебрежимо малым по сравнению с влиянием других сил, например, сил инерции и сил вязкого трения. В этих условиях вырожденным оказывается критерий Фруда, характеризующий соотношение сил инерции и гравитации, т.е. безразмерный перепад давления при обтекании автомобиля воздухом, определяющий его аэродинамическое сопротивление, является автомодельным по отношению к критерию Фруда.
Вопросы для самоконтроля 1. Смысл и содержание закона сохранения массы. 2. Смысл и содержание закона сохранения энергии. 3. Закон сохранения импульса и его частный случай – уравнение Навье-Стокса для потока жидкости. 4. Уравнение теплопроводности, физический смысл и размерность входящих в него теплофизических свойств. 5. Виды граничных условий, характеризующих теплообмен на поверхности тела с окружающей средой. 6. От чего зависят потери тепло через плоскую стенку? 7. Перечислите этапы вычислительного эксперимента. 8. Основы метода сеток. Конечно-разностная запись первой и второй производных. 9. Явная и неявная схемы аппроксимации уравнения теплопроводности. 10. Векторно-матричное представление сеточных уравнений. 11. Метод прогонки решения матричных уравнений и его реализация на компьютере. 12. Какие процессы называются подобными, чем они отличаются от аналогичных процессов? 13. Каково содержание трех теорем подобия? 14. Какой физический смысл имеет число Ньютона? 15. Получите критерий Пекле, каков его физический смысл? 16. Виды и структура движения воздуха, обтекающего автомобиль, число Рейнольдса, его физический смысл. 17. Каков смысл чисел Фруда и Эйлера? Приведите пример автомодельности при моделировании обтекания автомобиля воздухом. Основные понятия стохастического моделирования
Транспортный поток, движущейся по дорожной сети, состоит из множества автомобилей, которые управляются по более или менее свободному желанию водителей и маневры каждого автомобиля могут быть расценены как вероятностные события. Недетерминированной (вероятностной, стохастической) является такая модель, в которой функционирование отдельных элементов или входные значения зависят от случайных параметров, т.е. описываются законами распределения случайных величин. Результат функционирования такой модели может быть предсказан только в вероятностном смысле, т.е. представляет собой среднее значение (математическое ожидание) или закон распределения.
|


 , (6.59)
, (6.59)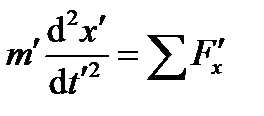 и для модели
и для модели 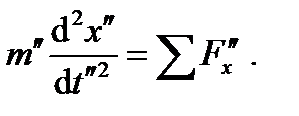 Введем константы подобия для входящих в уравнение (6.59) величин
Введем константы подобия для входящих в уравнение (6.59) величин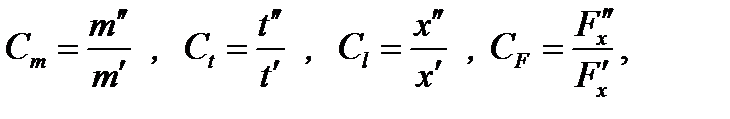
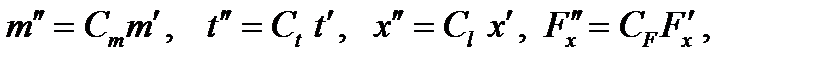
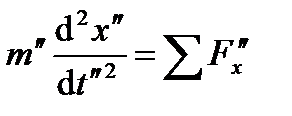


 .
. . (6.60)
. (6.60)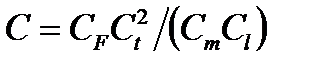 называется индикатором подобия, а вытекающее из (6.60) соотношение
называется индикатором подобия, а вытекающее из (6.60) соотношение (6.61)
(6.61)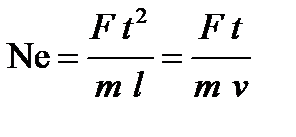 . (6.62)
. (6.62)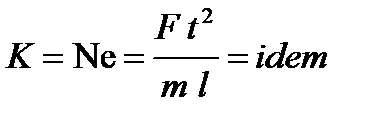 . (6.63)
. (6.63)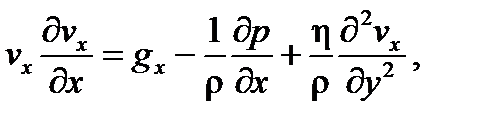 (6.64)
(6.64)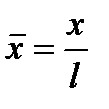 ,
, 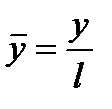 ,
, 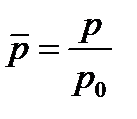 ,
, 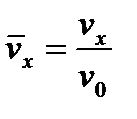 . (6.65)
. (6.65) ,
, 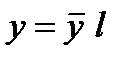 ,
,  ,
,  , и их дифференциалы
, и их дифференциалы 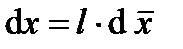 ,
, 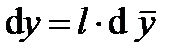 ,
, 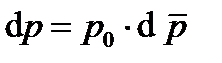 ,
, 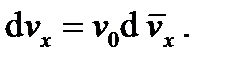

 получим
получим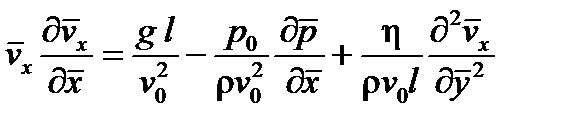 . (6.66)
. (6.66)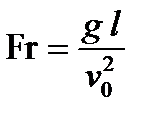 ,
, 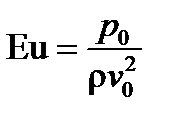 ,
, 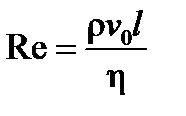 ,
, (6.67)
(6.67)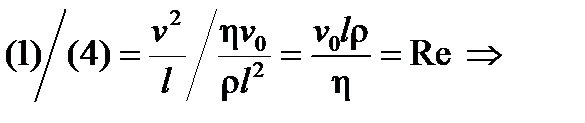
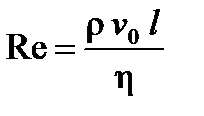
 ) силы вязкого трения преобладают над силами инерции, течение вязкой среды имеет слоистую, ламинарную структуру. При больших значениях числа Рейнольдса (
) силы вязкого трения преобладают над силами инерции, течение вязкой среды имеет слоистую, ламинарную структуру. При больших значениях числа Рейнольдса (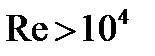 ), когда инерционные силы преобладают над силами вязкого трения, циркуляция вязкой среды имеет турбулентную структуру. Поперечные пульсации скорости и температуры при турбулентной конвекции приводят к возрастанию вязкости.
), когда инерционные силы преобладают над силами вязкого трения, циркуляция вязкой среды имеет турбулентную структуру. Поперечные пульсации скорости и температуры при турбулентной конвекции приводят к возрастанию вязкости.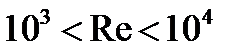 характеризует смешанный режим течения, при котором наблюдается примерное равенство сил инерции и вязкого трения и происходит смена ламинарного и турбулентного режимов течения.
характеризует смешанный режим течения, при котором наблюдается примерное равенство сил инерции и вязкого трения и происходит смена ламинарного и турбулентного режимов течения.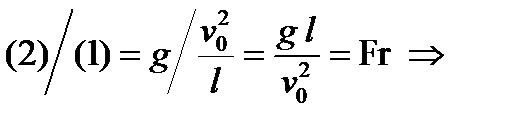
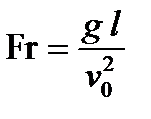 ,
,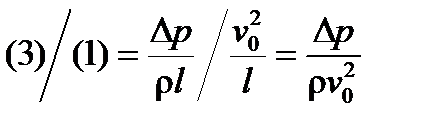
 , характеризующее отношение перепада давления к удвоенному динамическому напору (
, характеризующее отношение перепада давления к удвоенному динамическому напору (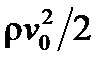 ), т.е. безразмерный перепад давления.
), т.е. безразмерный перепад давления. . (6.68)
. (6.68)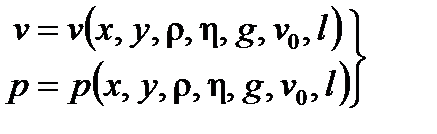 . (6.69)
. (6.69)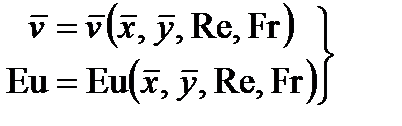 , (6.70)
, (6.70) и число Эйлера Eu – определяемыми.
и число Эйлера Eu – определяемыми.


