Функция и плотность распределения случайной величины
Опыт – это осуществление какого-нибудь комплекса условий, который может быть воспроизведен много раз. Под событием понимается результат опыта или наблюдения. События могут быть элементарными (неразложимыми) и составными (разложимыми). Элементарное событие происходит в результате единичного опыта. Составное событие – это совокупность элементарных событий. Пример 7.1. Игральный кубик подбрасывается 2 раза. Пусть составное событие определено следующим образом: «сумма выпавших цифр равна 6». Тогда элементарными будут события «5+1», «4+2», «3+3», «2+4» и «1+5». Любые другие сочетания не относятся к рассматриваемому составному событию. Генеральной совокупностью называют совокупность событий, которые могут быть реализованы в результате бесконечного числа однотипных опытов. Выборочной совокупностью или выборкой называют совокупность случайно отобранных событий из генеральной совокупности. Объемом совокупности называют число событий N этой совокупности. Случайной величиной называют переменную величину, которая в результате опыта может принимать различные значения. Случайные величины обычно обозначают большими буквами, например Х. Значения случайной величины, которые она принимает в результате опыта, обозначают малыми буквами Вероятностью некоторого события – это мера его «благоприятствия». События называются равновозможными, если мера их «благоприятствия» одинакова. В этом случае частость W события A: W (A) определяется формулой W (A) =n /N. (7.1) Вероятность р(А) произвольного события А изменяется от 0 до 1. При этом нулевая вероятность соответствует невозможному событию (которое никогда произойти не может), а единичная – достоверному событию (которое обязательно произойдет). При больших выборках вероятность события равна его частости р(А)≈W (A).(7.2) Для независимых событий вероятность произведения равна произведению их вероятностей (теорема умножения)
Пример 7.2. Надежность автомобиля зависит от многих факторов: надежности двигателя, электрической системы, качества бензина и других. Пусть вероятность работоспособного состояния автомобиля «по вине» двигателя р 1=0,99; по «вине» электрической системы р 2=0,98; по качеству бензина р 3=0,97. Необходимо оценить надежность автомобиля в целом, т.е. определить вероятность его работоспособного состояния ра. Решение. По формуле (3.3) ра = р 1 × р 2 × р 3=0,99 × 0,98 × 0,97 = 0,94. Для несовместных событий (они не могут наступить одновременно) справедлива теорема сложения вероятностей
Из этой теоремы вытекают два следствия: 1. Для полной группы несовместных событий сумма их вероятностей равна единице:
2. Сумма вероятностей противоположных событий равна единице
Пример 7.3. Видеокамера зафиксировала, что 75% водителей не нарушают скоростной режим (р (А)=0,75). Здесь событие А состоит в выборе автомобилей, не нарушающих установленный скоростной режим. Противоположное ему событие, отражающее долю нарушителей скоростного режима, будет Законом распределения случайной величины называют любое правило (таблицу, функцию), позволяющее находить вероятности всевозможных событий. Случайные величины бывают дискретными и непрерывными. Дискретными случайными величинами называют такие, которые могут принимать конечное и счетное множество возможных значений. Непрерывными случайными величинами называют такие, которые в некотором интервале могут принимать любое значение. Число автомобилей транспортного потока в различных выборках из генеральной совокупности есть дискретная случайная величина, а расстояния между ними – непрерывная случайная величина.
Распределение случайной величины X, называется интегральной функцией распределения F (xi) (см. рис. 7.3). Она определяет вероятность того, что случайная величина примет значения, не превосходящие хi, т.е. попадет в интервал F (xi) = р (X<xi). Задание F (xi) и определяет закон распределения случайной величины Х. В большинстве практически важных случаев распределение случайных величин может быть задано в другой форме с помощью введения функции плотности вероятностейf (x) (дифференциальной функции распределения). Характерной особенностью случайной величины является то, что заранее неизвестно, какое из значений она примет. Возможность принятия случайной величиной Х значения из интервала (х 1, х 2) количественно оценивается вероятностью р (x 1 <X где р (x 1 <X £ x 2) – вероятность указанного события (x 1< X £ x 2); f (х) - плотность распределения случайной величины; x 2= x 1+d х. Плотность вероятности является важнейшей характеристикой, задающей распределение случайной величины, Плотность удовлетворяет двум условиям: она неотрицательна и интеграл от нее в полных пределах изменения аргумента х равен единице:
Функция распределения F (х) выражается через плотность f (х):
С другой стороны, если плотность f (х) непрерывна в точке х, то ее значение в этой точке равно производной от функции F (х):
Функция распределения F (x)является первообразной для плотности f (x), поэтому
f (x) называют также дифференциальной функцией распределения. Свойства функции распределения: она неотрицательна, возрастающая и равна 0 и 1 при значении аргумента –¥ и ¥: F (х)³0; F (х 1) < F (х 2)при x 1 < х 2; F (–
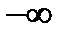 < х 0 <+ < х 0 <+  число F (x 0)равно площади под кривой распределения, лежащей левее прямой X=х 0. Аналогично интерпретируется вероятность р (x 1 <; x число F (x 0)равно площади под кривой распределения, лежащей левее прямой X=х 0. Аналогично интерпретируется вероятность р (x 1 <; x 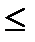 x 2). x 2).
Случайная величина x, для которой существует плотность распределения f (x), называется непрерывной. Если под случайной величиной x понимать скорость движения автомобиля, то произведение f (х)d х есть вероятность его движения со скоростью в интервале (х 1, х 2).Значение функции распределения F (х) равно вероятности движения автомобиля со скоростью от 0 до х. В теории надежности часто употребляют такое понятие, как вероятность безотказной работы р (х), которое является дополнительным понятием к функции распределения F (x), здесь переменная x характеризует уже время эксплуатации автомобиля. Значение вероятности безотказной работы в точке х равно вероятности того, что случайная величина X превыситх, т. е. автомобиль будет работать безотказно в течение времени x: р (х) = 1– F (х)= р { X>; х }.
Функция р (х) называется также функцией надежности. Примерные графики функции распределения F (х)и функции надежности р (х)изображены на рис. 7.5.
|

 При массовых испытаниях каждое из возможных значений случайной величины
При массовых испытаниях каждое из возможных значений случайной величины 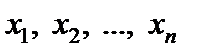 может встретиться m 1, m 2, …, mn раз. Эти числа называют частотами. Весь набор значений случайной величины образует генеральную совокупность N x. Отсеянные из генеральной совокупности N x значения грубых ошибок образуют выборку объемом N. Если всего было проведено N x опытов, то в результате выборки получаем
может встретиться m 1, m 2, …, mn раз. Эти числа называют частотами. Весь набор значений случайной величины образует генеральную совокупность N x. Отсеянные из генеральной совокупности N x значения грубых ошибок образуют выборку объемом N. Если всего было проведено N x опытов, то в результате выборки получаем 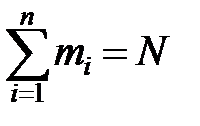 , и отношение mi /N называют частостью или относительной частотой.
, и отношение mi /N называют частостью или относительной частотой.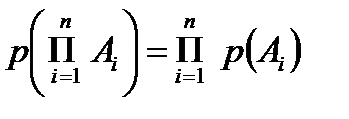 (7.3)
(7.3)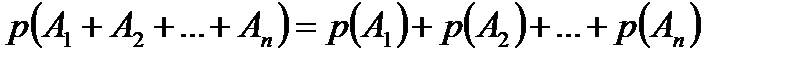 . (7.4)
. (7.4)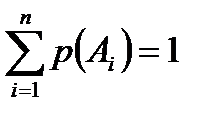 . (7.5)
. (7.5) . (7.6)
. (7.6) . По формуле (7.6) находим
. По формуле (7.6) находим  , т.е. 25% автомобилей двигались с превышением установленной скорости.
, т.е. 25% автомобилей двигались с превышением установленной скорости.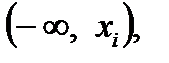
 . (7.8)
. (7.8)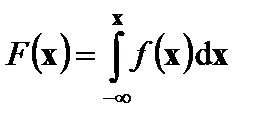 . (7.9)
. (7.9)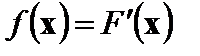 . (7.10)
. (7.10)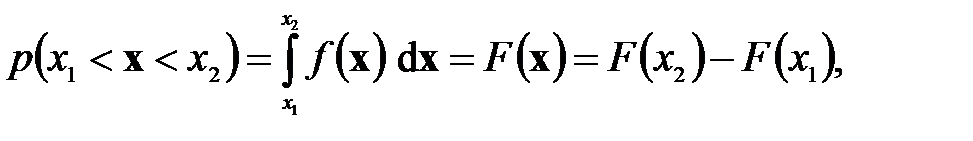 (7.11)
(7.11)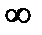 ) = 0; F (
) = 0; F (


