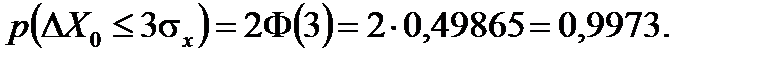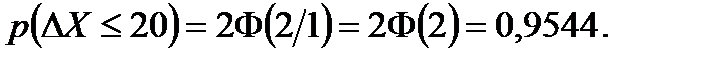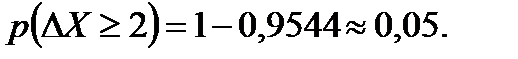Кривая Гаусса имеет следующие особенности.
1. Кривая симметрична относительно 2. При
3. На расстоянии ±σ от вершины кривая имеет две точки перегиба А и Б, координаты которых равны:
4. На расстоянии ±3σ от вершины кривой ее ветви так близки к оси абсцисс, что в пределах ±3σ 99,7 % всей площади ограничивается кривой. Практически принято считать, что на расстоянии ±3σ от вершины кривой ее ветви пересекаются с осью абсцисс, и в этих пределах заключена вся площадь кривой, т.е. 100,0%. Отклонения в этом случае составляет 0,3%, что допустимо при решении многих практических задач. 5. σ – это мера рассеяния, мера точности. На основании п.4 справедливо утверждение, что поле рассеяния ω≈6σ. С использованием закона Гаусса вероятный процент автомобилей, движущихся в заданном интервале скоростей, вычисляется следующим образом. Считаем, что все автомобили движутся со скоростями в пределах поля рассеяния
где x max, x min – максимальное и минимальное значения параметра (скорости). При этом площадь, ограниченная кривой нормального распределения и осью абсцисс, равна единице и определяет 100% автомобилей. Площадь заштрихованных на рис. 7.10 участков представляет собой количество автомобилей, скорость движения которых выходит по своим значениям за пределы допускаемой правилами дорожного движения. Для определения количества автомобилей, движущихся по правилам, необходимо найти площадь, ограниченную кривой и осью абсцисс на длине, равной допуску δ. При симметричном расположении поля рассеяния относительно поля допуска следует найти значение интервала, определяющего половину площади, ограниченной кривой Гаусса и абсциссой х 1 (х 2). Функция распределения для нормального закона имеет вид (рис. 7.11)
Для случая, когда
Таким образом, если случайная величина Х следует закону нормального распределения, то вероятность появления случайной погрешности определяется площадью, ограниченной кривой f (x) и ее частью и осью абсцисс:
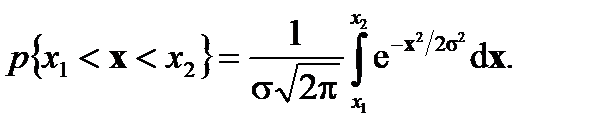 (7.26) (7.26)
Подынтегральное значение есть элемент вероятности, равный площади прямоугольника с основанием d x и абсциссами x 1 и x 2, называемыми квантилями. Произведем замену переменной: t= x / s,d x = s × d t:
Представим правую часть в виде суммы двух интегралов:
Интеграл вида
носит название нормальной функции Лапласа. Значения этого интеграла сведены в таблицу. Таким образом, указанная вероятность (7.28) сводится к разности нормальных функций Лапласа: р { x 1 < x < x 2 } = Ф (t 2) – Ф (t 1). (7.29) Расчет количества автомобилей, движущихся в заданном интервале скоростей, сводится к установлению величины t и определению Ф(t) по таблице с последующим пересчетом полученных величин в проценты или в число автомобилей. В общем случае, когда
Отметим свойства функции Лапласа: Ф(0) = 0; Ф(– х) = –Ф(х)(функция нечетная); Ф( Пример 7.5. При измерении скорости автомобилей на участке дороги установлено, что скорость (случайная величина x) распределена нормально с математическим ожиданием 80 км/ч и средним квадратичным отклонением 10 км/ч. Необходимо найти вероятность того, что скорость автомобилей заключена в пределах 30…90 км/ч, оговоренных правилами дорожного движения. Решение. Используем формулу (7.29). По условию задачи x 1=30; x 2=90;
По таблице функции Лапласа находим: Ф(1,0)=0,3413; Ф(5,0)=0,4999. Отсюда искомая вероятность Таким образом, только 84% автомобилей на этом участке дороги соблюдают оговоренный правилами скоростной режим. Во многих практических задачах требуется вычислить вероятность того, что абсолютное отклонение Δ X нормально распределенной случайной величины X от математического ожидания меньше заданного положительного числа ε, т.е. требуется найти вероятность выполнения неравенства
На основании нечетности функции Лапласа справедливо соотношение
Аналогично для нормированной случайной величины
Обозначив Если t =3 и соответственно
Вероятность того, что абсолютное отклонение будет меньше утроенного среднеквадратичного отклонения, равна 0,9973 и большие отклонения практически невозможны. В этом состоит «правило трех сигм»: при нормальном распределении случайной величины абсолютная величина ее отклонения от математического ожидания не превышает утроенного среднего квадратичного отклонения. Это правило применяют для проверки нормальности распределения изучаемой величины и для выявления грубых ошибок (промахов) в экспериментальных данных. Пример 7.6. При измерении скорости автомобилей на участке дороги установлено, что скорость (случайная величина x) распределена нормально со средним квадратичным отклонением 20 км/ч. Необходимо найти вероятность доли автомобилей, превышающих максимально допустимую скорость на 20 км/ч. Решение. Используем формулу (7.32). По условию задачи ε=20 км/ч, s x =10 км/ч, следовательно, вероятность доли автомобилей, соблюдающих скоростной режим
Вероятность доли автомобилей, превышающих максимально допустимую скорость на 20 км/ч, равна вероятности противоположного события
|

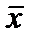 .
.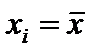 кривая имеет максимум:
кривая имеет максимум: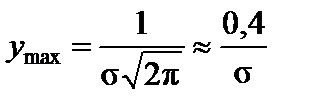 .
. .
.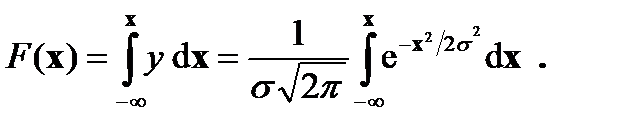 (7.24)
(7.24)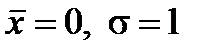 , распределение называют стандартным и функция распределения имеет следующий вид:
, распределение называют стандартным и функция распределения имеет следующий вид: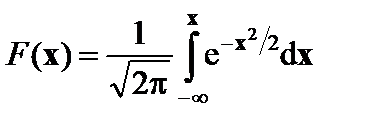 . (7.25)
. (7.25)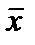
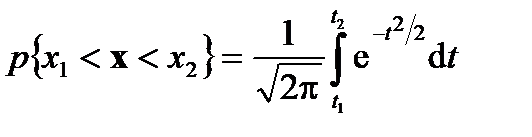 . (7.27)
. (7.27)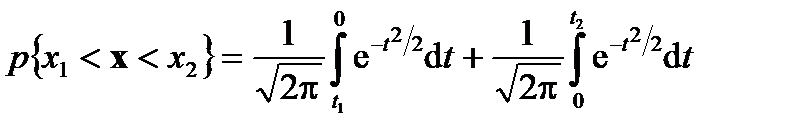 .
.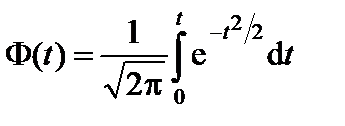 (7.28)
(7.28)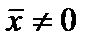 , имеем следующую вероятность появления случайных погрешностей:
, имеем следующую вероятность появления случайных погрешностей: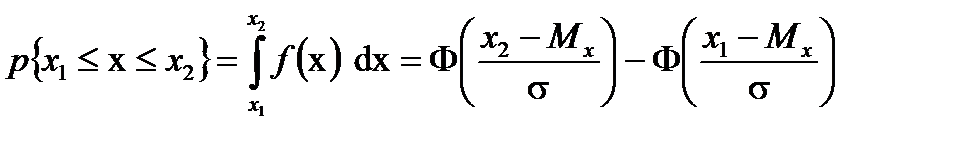 . (7.30)
. (7.30) )=1/2. Из рис. 7.11 видно, что кривые F (х) и Ф(x) эквидистантны.
)=1/2. Из рис. 7.11 видно, что кривые F (х) и Ф(x) эквидистантны.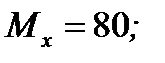 s=10, следовательно,
s=10, следовательно,
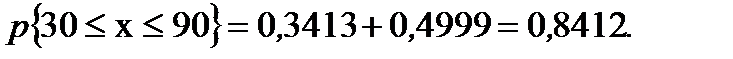
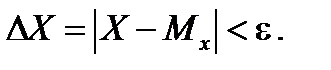 (7.31)
(7.31)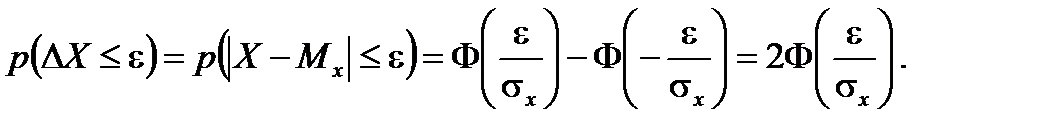 (7.32)
(7.32)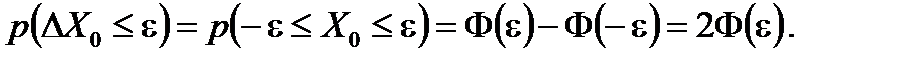 (7.33)
(7.33)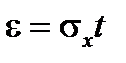 , получим
, получим 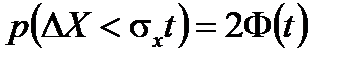 .
.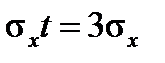 , то
, то