Целью моделирования любого процесса является установление количественной зависимости выходного параметра от одного или группы случайных входных параметров. Например, выбор водителем скорости движения транспортного средства зависит от многих факторов: вида транспортного средства, состояния дорожного покрытия, числа полос, самочувствия самого водителя и других факторов. В функциональной связи Y = f (X) каждому значению независимой переменной X отвечает одно или несколько вполне определенных значений зависимой переменной Y. В этом случае связь между переменными X и Y в отличие от функциональной приобретает статистический характер и называется корреляционной.
Простейшей и распространенной зависимостью между величинами X и Y является линейная регрессия. Оценка тесноты или силы связи между величинами X и Y осуществляется методами корреляционного анализа.
Рассмотрим линейную регрессию от одного параметра (рис. 7.17). Пусть для произвольного фиксированного значения x получено несколько значений y. Предполагается, что величина Y распределена нормально с математическим ожиданием
| Рис. 7.17. Корреляционное поле зависимости
Y = f (X) с эмпирической (1) и теоретической
(2) линиями регрессии
|

(7.35)
и дисперсией  , не зависящей от X. Из (7.35) видно, что случайная величина Y в среднем линейно зависит от фиксированного значения x, а параметры
, не зависящей от X. Из (7.35) видно, что случайная величина Y в среднем линейно зависит от фиксированного значения x, а параметры 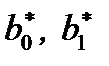 и
и  являются неизвестными параметрами генеральной совокупности.
являются неизвестными параметрами генеральной совокупности.
Для оценки этих неизвестных величин по выборке объемом n сопряженных пар значений x 1, y 1; x 2, y 2; …; xn, yn в декартовой системе координат можно построить корреляционное поле, содержащее n точек. Если нанести на поле средние значения 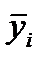 , соответствующие всем значениям переменной xi в интервалах, ограниченных вертикальными линиями координатной сетки, то зависимость y от x станет более очевидной.
, соответствующие всем значениям переменной xi в интервалах, ограниченных вертикальными линиями координатной сетки, то зависимость y от x станет более очевидной.
Ломаная линия, соединяющая точки 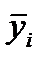 , отнесенные к серединам интервалов x ср i , называется эмпирической линией регрессии. С увеличением числа опытов ломаная линия сглаживается и приближается к предельной линии – теоретической линии регрессии.
, отнесенные к серединам интервалов x ср i , называется эмпирической линией регрессии. С увеличением числа опытов ломаная линия сглаживается и приближается к предельной линии – теоретической линии регрессии.
 (7.35)
(7.35)

 , не зависящей от X. Из (7.35) видно, что случайная величина Y в среднем линейно зависит от фиксированного значения x, а параметры
, не зависящей от X. Из (7.35) видно, что случайная величина Y в среднем линейно зависит от фиксированного значения x, а параметры 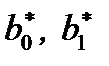 и
и 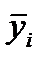 , соответствующие всем значениям переменной xi в интервалах, ограниченных вертикальными линиями координатной сетки, то зависимость y от x станет более очевидной.
, соответствующие всем значениям переменной xi в интервалах, ограниченных вертикальными линиями координатной сетки, то зависимость y от x станет более очевидной.


