Меры положения и рассеяния кривой распределения
Кривая распределения плотностей вероятностей случайной величины характеризуется своим положением на оси абсцисс и рассеиванием случайной величины. Для оценки положения и рассеяния кривой распределения вводятся соответствующие критерии или меры. К мерам положения относятся: мода, математическое ожидание и медиана случайной величины. К мерам рассеяния относятся: дисперсия, стандартное отклонение и размах. Модой распределения (Mо) называется наиболее вероятное значение случайной величины X. Плотность вероятности f (x)принимает максимальное значение в окрестности моды. Функция распределения плотности вероятностей может иметь одно или несколько максимальных значений в разных местах области (рис. 7.6). Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений:
 (7.12) (7.12)
Математическое ожидание случайной величины X, имеющей плотность распределения f (х), вычисляется по формуле
Статистической оценкой математического ожидания является среднее арифметическое значение случайной величины
где N – количество значений xi; mi – частота появления результата xi. Математическое ожидание (среднее арифметическое значение) случайной величины называют часто центром рассеяния или центром группирования случайной величины. Математическое ожидание является оценкой истинного значения измеряемой величины. Пример 7.4. Найти математическое ожидание и моду случайной величины, заданной таблицей значений
Решение. Медианой случайной величины (Ме) называется такое ее значение х, для которого
т. е. вероятность появления случайной величины меньшей, чем медиана, или большей, чем медиана, одинакова. Геометрическая медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 7.7):
Мерой рассеяния случайной величины Х около ее среднего значения
Для непрерывной случайной величины s определяется по формуле
Другая мера рассеяния – дисперсия (дисперсия и означает рассеивание) характеризует разброс значений случайной величины относительно ее математического ожидания. Дисперсия увеличивается с увеличением рассеяния результатов наблюдения. Дисперсия определяется по формуле
где хi - дискретная случайная величина, и по формуле
где хi – непрерывная случайная величина. Свойства дисперсии: · Д х ≥ 0; · Д х ∙ С = 0 для С = const (дисперсия неслучайной величины равна нулю); · Д(СХ) = С 2∙Д х – неслучайную величину можно выносить за знак дисперсии, возведя ее в квадрат; · Д х = М x (X 2) – (М х)2 – дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания; · Д(Х + Y) = Д х + Д y,если Х и Y – независимые случайные величины. Последнее свойство рассмотрим более подробно на примере двух случайных величин X и Y. По определению
После раскрытия квадратных скобок и объединения каждой случайной величины со своим математическим ожиданием получим
откуда
где
Коэффициент корреляции меняется в пределах от –1 до +1 и является характеристикой тесноты линейной связи между двумя случайными величинами. Если xи y независимы, то Размах случайной величины R определяется как разность между наибольшим и наименьшим значениями случайной величины:
|

 . (7.13)
. (7.13) ,(7.14)
,(7.14)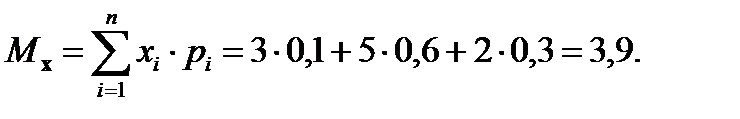


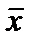 служит стандартное (или среднее квадратичное) отклонение s:
служит стандартное (или среднее квадратичное) отклонение s: (7.16)
(7.16)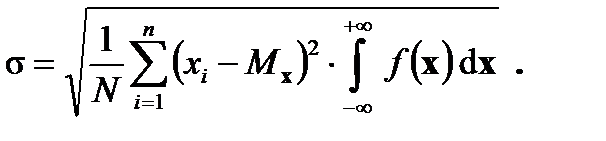 (7.17)
(7.17) (7.18)
(7.18)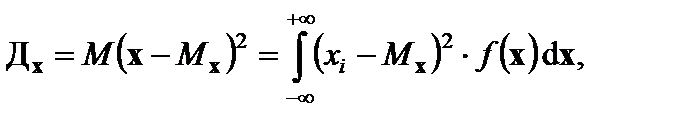 (7.19)
(7.19) .
.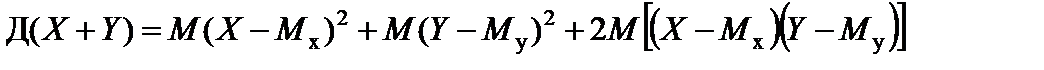 ,
, ,
, – ковариация. Она характеризует связь между случайными величинами X и Y. Для независимых случайных величин ковариация равна нулю. Ковариация является неудобной характеристикой, так как по ее величине трудно судить о степени (тесноте) связи. Поэтому была введена другая величина – коэффициент корреляции, вычисляемый по формуле
– ковариация. Она характеризует связь между случайными величинами X и Y. Для независимых случайных величин ковариация равна нулю. Ковариация является неудобной характеристикой, так как по ее величине трудно судить о степени (тесноте) связи. Поэтому была введена другая величина – коэффициент корреляции, вычисляемый по формуле . (7.20)
. (7.20) . Если абсолютное значение ρ(ХY) окажется больше 1, то совершенно ясно, что произошла ошибка и необходимо пересчитать результат. В случае сильной положительной корреляции достигается значение, близкое к +1, а при сильной отрицательной корреляции достигается значение, близкое к –1. Таким образом, когда |ρ(ХY)| близок к 1, это указывает на сильную корреляцию между X и Y, а когда |ρ(ХY)| близок к 0 – на слабую корреляцию.
. Если абсолютное значение ρ(ХY) окажется больше 1, то совершенно ясно, что произошла ошибка и необходимо пересчитать результат. В случае сильной положительной корреляции достигается значение, близкое к +1, а при сильной отрицательной корреляции достигается значение, близкое к –1. Таким образом, когда |ρ(ХY)| близок к 1, это указывает на сильную корреляцию между X и Y, а когда |ρ(ХY)| близок к 0 – на слабую корреляцию. (7.21)
(7.21)


