Подобие физических явлений
Одним из средств решения задач моделирования транспортных систем, обобщения экспериментальных и расчетных данных является теория подобия и моделирования. Теория подобия (учение о подобных явлениях) дает общий метод преобразования выражений, содержащих дифференциальные операторы, к алгебраическим уравнениям. Суть метода в том, что реальный процесс заменяется условной схемой (моделью), в которой все дифференциальные операторы сохраняют постоянное значение в пространстве и во времени. Термин «подобие» заимствован из геометрии. Так, для подобных фигур (рис. 6.4)
где Сl – константа геометрического подобия, или коэффициент пересчета масштабов, зная который, можно получить любой размер в одной системе по сходственному размеру в другой. Следствием геометрического подобия является соответственное выражение для площадей (S) и объемов (V)
   . (6.57) . (6.57)
На практике при геометрическом подобии используются не характеристики размеров объекта и модели, а их координаты. Если ввести систему прямоугольных координат x, y, то при геометрическом подобии все координаты
Этот пример иллюстрирует дальнейшее развитие понятия подобие – аффинное подобие, при котором допускается неравенство масштабов по отдельным координатным осям. В этом случае геометрические фигуры или пространственные объекты как бы деформируются: круг превращается в эллипс, параллелепипед с неравномерными ребрами – в куб и т.п. Переход к аффинному подобию возникает, например, при моделировании сил сопротивления воздушного потока движению транспортного средства, когда размер пограничного слоя воздуха у поверхности транспортного средства, в котором реализуются силы сопротивления, мал по сравнению с размерами транспортного средства. Преобразующие функции (6.58), осуществляющие взаимосвязь между координатами модели и объекта, могут быть и нелинейными. Для реализации подобия физических явлений геометрического подобия недостаточно, необходимо соблюдение подобия и по другим характеристикам, определяющим эти явления: времени, скоростям, массам, силам, температурам, и т.д. Рассмотрим основные понятия подобных явлений. Одноименными величинами называются такие, которые имеют одинаковые физический смысл и размерность (например, скорость объекта и модели). Сходственными точками системы называются такие точки, координаты которых удовлетворяют условию геометрического подобия (6.56). Сходственные моменты времени наступают по истечении периодов времени Подобными называются физические явления, протекающие в геометрически подобных системах, если у них во всех сходственных точках в сходственные моменты времени отношения одноименных величин есть постоянные числа. Эти постоянные числа называются числами подобия. Следует отметить, что подобными могут быть явления одинаковой природы, описывающиеся одинаковыми аналитическими зависимостями. Явления, описываемые одинаковыми уравнениями, но имеющие различную природу, называются аналогичными. Пример аналогичных явлений: движение потока жидкости в каналах и транспортного потока по дороге.
|

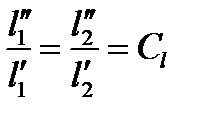 , (6.56)
, (6.56)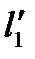



 объекта пропорциональны соответствующим координатам
объекта пропорциональны соответствующим координатам  модели, т.е. выполняются соотношения
модели, т.е. выполняются соотношения ;
;  , (6.58)
, (6.58) , имеющих общее начало отсчета и связанных между собой константой подобия
, имеющих общее начало отсчета и связанных между собой константой подобия  .
.


