Моделирование тепловых систем
Процесс переноса тепловой энергии (теплоты) в пространстве с неоднородным полем температуры называется теплообменом. Теплообмен может осуществляться теплопроводностью, конвекцией и тепловым излучением. Температурным полем называется совокупность значений температуры для всех точек пространства в данный момент времени. Температурное поле скалярное, так как температура – скалярная величина. Если температура Т является функцией только пространственных координат Т(х, у, z), то процесс теплообмена стационарный и температурное поле стационарное. Если температура изменяется во времени, то процесс теплообмена и температурное поле нестационарные. Соединив точки теплотехнического объекта, имеющие одинаковую температуру, получим поверхность равных температур, называемую изотермической. При проектировании теплотехнических объектов на микроуровне используют уравнение теплопроводности, связывающее изменение температуры во времени и пространстве со свойствами среды. Это уравнение позволяет выполнять анализ температурных полей в твердых телах – деталях машин. Уравнение теплопроводности является частным случаем закона сохранения энергии. Применительно к тепловой системе закон сохранения энергии можно сформулировать так: изменение во времени количества тепловой энергии в элементарном объеме равно сумме притока-стока энергии через его поверхность с учетом выделения энергии в том же объеме в единицу времени внутренними источниками (или поглощения энергии стоками). По аналогии с уравнением (6.8) можно записать
где Q – количество тепловой энергии в единице объема, Дж/м3; Выделение (или поглощение) тепловой энергии внутри тела может происходить из-за объемных химических реакций, прохождения электрического тока, фазовых превращений материала при изменении температуры и т.п. Величина GQ характеризует мощность внутренних источников (или стоков) теплоты. Изменение количества тепловой энергии в единице объема dQ пропорционально изменению температуры dT:
где c – удельная теплоемкость материала теплотехнического объекта, Дж/(кг∙К); ρ – плотность материала. Уравнение (6.12) называется уравнением переноса тепловой энергии. Если плотность теплового потока
где λ – коэффициент теплопроводности материала, Вт/(м∙К); С учетом выражений (6.13) и (6.14) при λ=const уравнение (6.12) приводится к виду
где ат = λ/(cρ) – коэффициент температуропроводности, м2/с, характеризующий теплоинерционные свойства тела. Для одномерного случая, когда теплопередача осуществляется только вдоль оси х, уравнение теплопроводности (6.15) принимает вид
а при отсутствии еще и источника тепла (GQ=0)
При решении уравнений (6.15), (6.16) должна быть задана функция GQ= GQ(x, y, z, t) и краевые условия – начальные и граничные. Кроме того, необходимо описание геометрии теплотехнического объекта (его формы и размеров), а также физических свойств объекта и среды (значений параметров ρ, λ, c). Временные или начальные условия характеризуют распределение температуры в объекте в начальный момент времени. Для стационарных задач эти условия отсутствуют. Граничные краевые условия теплообмена характеризуют форму тела и условия его теплообмена с окружающей средой. Различают четыре вида граничных условий теплообмена. При граничных условиях 1 -го вида на поверхности тела для каждого момента времени задается распределение температуры
В частном случае температура поверхности может поддерживаться постоянной во времени, такая граница называется изотермической: При граничных условиях 2 -го вида на поверхности тела для каждого момента времени задается плотность теплового потока
В частном случае плотность теплового потока может поддерживаться постоянной во времени, При граничных условиях 3 -го вида на поверхности тела для каждого момента времени задается температура окружающей среды и закон конвективного теплообмена между поверхностью тела и окружающей средой
где α – коэффициент теплоотдачи, характеризующий плотность теплового потока при единичной разности температур между поверхностью тела и окружающей средой, Вт/(м2∙К). Отметим, что граничные условия 1-го и 2-го рода являются частными случаями граничных условий конвективного теплообмена: 1. 2. Граничные условия 4 -го вида описывают условия теплообмена на границе контакта двух тел
где R к [К·м2/Вт] – тепловое сопротивление контакта, зависящее от давления, чистоты поверхностей и других факторов, Δ Т = Т п1– Т п2 – перепад температур на контактирующих поверхностях. В частном случае идеального контакта (R к=0)
т.е. коэффициент теплопроводности и температурный градиент обратно пропорциональны: чем выше коэффициент теплопроводности материала, тем меньше в нем температурный градиент. Дифференциальное уравнение теплопроводности вместе с краевыми условиями дают формулировку краевой задачи теплопроводности в объекте, имеющую единственное решение. В частном случае стационарной теплопроводности плоского слоя толщиной δ, не содержащего внутренних источников тепла (GQ=0), на поверхностях которого x =0 и x =δ заданы граничные условия первого рода, т.е. поддерживаются температуры соответственно Т 1 и Т 2, математическая формулировка краевой задачи имеет вид
Общее решение уравнения теплопроводности (6.23) получается после двойного интегрирования
Постоянные интегрирования С 1 и С 2 находятся подстановкой граничных условий (6.23) в общее решение (6.24)
В результате получается решение задачи
дающее линейное распределение температуры по толщине слоя. Плотность теплового потока определяется в соответствии с законом Фурье (6.14)
и является постоянной, отношения Потери тепла через плоскую стенку
Пример 6.1. Определить потери тепла через кирпичную стенку ( Решение. По формуле (6.27) определяем потери тепла через кирпичную стенку
потери тепла через деревянную стенку
Один кВт·час тепловой энергии составляет 3600 Дж, следовательно, стоимость потерь через кирпичную стенку составляет 2∙62500/3600=34,8 руб, а через деревянную стенку – 2∙22200/3600=12,4 руб, что почти в 3 раза меньше.
|

 (6.12)
(6.12)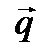 – вектор плотности теплового потока, Вт/м2; GQ – количество тепловой энергии, выделяемой в единицу времени в рассматриваемом элементарном объеме, Вт/м3.
– вектор плотности теплового потока, Вт/м2; GQ – количество тепловой энергии, выделяемой в единицу времени в рассматриваемом элементарном объеме, Вт/м3.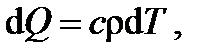 (6.13)
(6.13)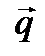 подчиняется закону теплопроводности (закон Фурье), то уравнение переноса тепловой энергии переходит в уравнение теплопроводности. В соответствии с законом Фурье плотность теплового потока пропорциональна градиенту температуры:
подчиняется закону теплопроводности (закон Фурье), то уравнение переноса тепловой энергии переходит в уравнение теплопроводности. В соответствии с законом Фурье плотность теплового потока пропорциональна градиенту температуры: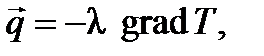 (6.14)
(6.14)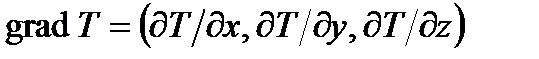 – градиент температуры.
– градиент температуры. (6.15)
(6.15) (6.16)
(6.16)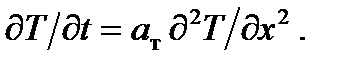 (6.17)
(6.17) (6.18)
(6.18) .
. (6.19)
(6.19)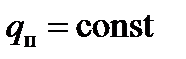 , либо быть нулевой, в последнем случае граница называется адиабатной.
, либо быть нулевой, в последнем случае граница называется адиабатной.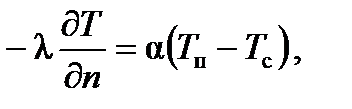 (6.20)
(6.20)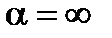
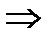
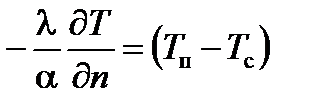

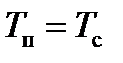 – изотермическая граница;
– изотермическая граница;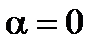
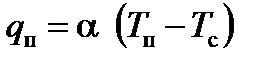
 – адиабатная граница.
– адиабатная граница. , (6.21)
, (6.21) , (6.22)
, (6.22)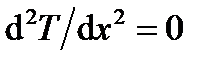 , …
, …  (6.23)
(6.23)
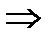
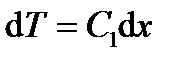
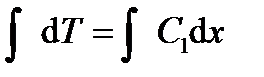
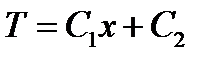 . (6.24)
. (6.24)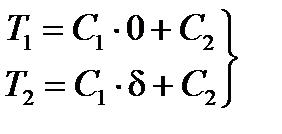 и имеют вид
и имеют вид 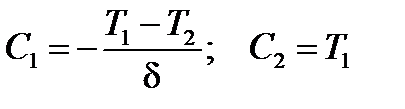 .
. , (6.25)
, (6.25)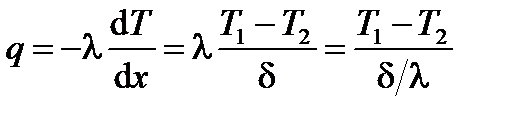 (6.26)
(6.26) и
и  называются соответственно тепловой проводимостью и тепловым сопротивлением плоского слоя.
называются соответственно тепловой проводимостью и тепловым сопротивлением плоского слоя.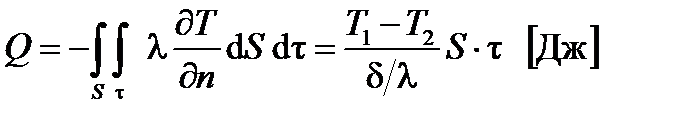 . (6.27)
. (6.27)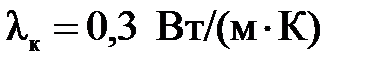 ) площадью 3х5 м за сутки. Как изменится теплопроводность, если кирпичную стенку заменить деревянной (сосна поперек волокон,
) площадью 3х5 м за сутки. Как изменится теплопроводность, если кирпичную стенку заменить деревянной (сосна поперек волокон,  ). Толщины стенок составляют δк= δд=25 см, температуры наружной и внутренней поверхностей стенки соответственно t 1= 20oC, t 2= –20oC. Определить стоимость потерь при цене 1 кВт·час энергии 2 руб.
). Толщины стенок составляют δк= δд=25 см, температуры наружной и внутренней поверхностей стенки соответственно t 1= 20oC, t 2= –20oC. Определить стоимость потерь при цене 1 кВт·час энергии 2 руб.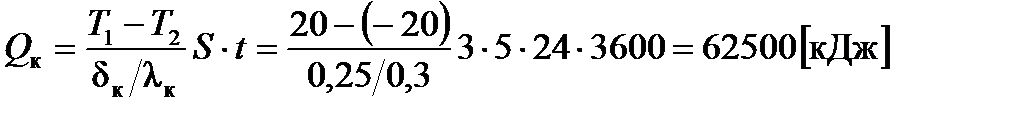 ,
,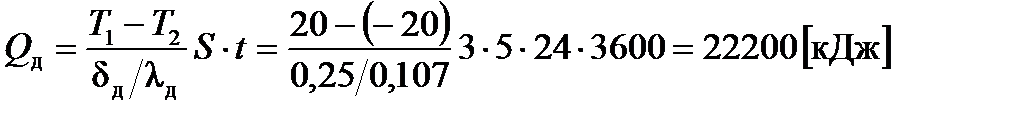 .
.


