Основы построения математических моделей на микроуровне
Для построения математических моделей технических объектов с распределенными параметрами используют фундаментальные физические законы. К ним относятся, прежде всего, законы сохранения (массы, энергии, импульса). Общая формулировка закона сохранения: изменение во времени некоторой субстанции в элементарном объеме равно сумме притока-стока этой субстанции через его поверхность с учетом скорости генерации или уничтожения субстанции в этом объеме. Уравнение, соответствующее данной формулировке, имеет вид
где φ – фазовая переменная (координата), выражающая субстанцию; У трехмерного технического объекта вектор
Дивергенция вектора плотности потока характеризует сумму притока-стока субстанции через поверхность элементарного объема. В качестве субстанции в различных физических законах выступают: масса, энергия, импульс и др. Уравнение закона сохранения массы
где ρ – плотность массы, кг/м3;
Уравнение (6.3) в гидроаэродинамике называют уравнением неразрывности. В одномерном случае, когда скорость направлена лишь вдоль оси х, уравнение (6.3) имеет вид
Плотность потока массы
где G, кг/c – массовый секундный расход в канале площадью поперечного сечения f. Из последнего уравнения следует постоянство расхода при стационарном течении в канале
а при течении несжимаемой среды (r=const) следует обратно пропорциональная зависимость между скоростью течения и площадью поперечного сечения канала: скорость возрастает в сужающихся и падает в расширяющихся участках канала. Уравнение закона сохранения энергии
где Е = е + v2/2 – полная энергия единицы массы; е – внутренняя энергия единицы массы; ρЕ – энергия единицы объема Дж/м3; В одномерном случае поток энергии направлен только вдоль оси х, тогда JE=JEx, а уравнение (6.6) принимает вид
Плотность потока энергии измеряется в Вт/м2. Уравнение закона сохранения импульса используют при моделировании движения потока жидкости (газа). Для потока идеальной жидкости (без учета сил трения, обусловленных вязкостью) уравнение имеет вид
где Градиентом называют векторную функцию скалярного аргумента. Компонентами вектора градиента являются частные производные аргумента по пространственным координатам. Градиент давления
Для одномерного потока жидкости из уравнения (6.8) получаем
При учете сил трения (
где g – ускорение свободного падения; η – динамическая вязкость Па∙с; Уравнение (6.10) называют уравнением Навье–Стокса. Для одномерного потока жидкости, движущейся в направлении оси x при поперечной силе трения (vx=vx(y)), это уравнение имеет вид:
где gx – проекция вектора
|

 (6.1)
(6.1) – вектор плотности потока фазовой переменной;
– вектор плотности потока фазовой переменной;  – дивергенция вектора
– дивергенция вектора  ; G – скорость генерации или уничтожения субстанции.
; G – скорость генерации или уничтожения субстанции.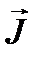 состоит из трех составляющих, направленных параллельно осям декартовой системы координат х, у, z. Дивергенция вектора
состоит из трех составляющих, направленных параллельно осям декартовой системы координат х, у, z. Дивергенция вектора  – скалярная величина, определяемая выражением
– скалярная величина, определяемая выражением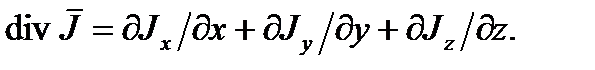 (6.2)
(6.2) (6.3)
(6.3) – вектор плотности потока массы:
– вектор плотности потока массы: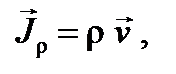 (6.4)
(6.4) – вектор скорости переноса массы.
– вектор скорости переноса массы. (6.5)
(6.5) измеряется в кг/(м2∙с). Из уравнения неразрывности (6.5) следует частный случай стационарного (
измеряется в кг/(м2∙с). Из уравнения неразрывности (6.5) следует частный случай стационарного ( ) одномерного течения по оси x в канале переменного сечения:
) одномерного течения по оси x в канале переменного сечения: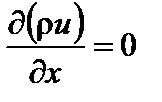 , откуда
, откуда 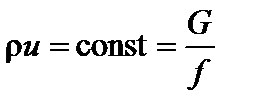 ,
,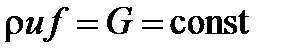 ,
, (6.6)
(6.6) – вектор плотности потока энергии; GЕ – скорость генерации или поглощения энергии в единице объема, Дж/(м3∙с).
– вектор плотности потока энергии; GЕ – скорость генерации или поглощения энергии в единице объема, Дж/(м3∙с).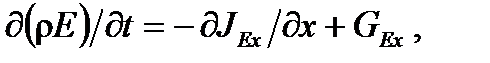 (6.7)
(6.7)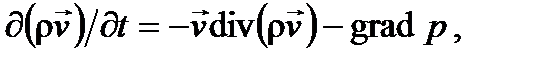 (6.8)
(6.8)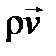 – вектор импульса единицы объема жидкости; р – давление жидкости; grad р – градиент давления.
– вектор импульса единицы объема жидкости; р – давление жидкости; grad р – градиент давления.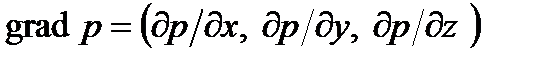 .
.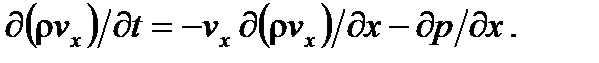 (6.9)
(6.9) ) и массовых сил (тяжести) уравнение закона сохранения импульса для несжимаемой среды (ρ=сonst) имеет вид
) и массовых сил (тяжести) уравнение закона сохранения импульса для несжимаемой среды (ρ=сonst) имеет вид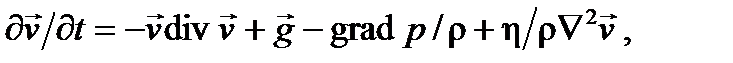 (6.10)
(6.10) – оператор Лапласа:
– оператор Лапласа:  .
.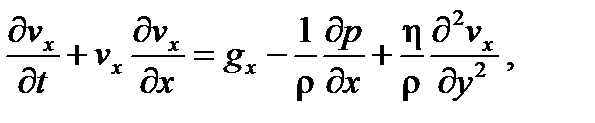 (6.11)
(6.11)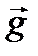 на ось x.
на ось x.


