Схемы аппроксимации уравнения теплопроводности
От аппроксимации отдельных производных перейдем к дискретному представлению всего уравнения теплопроводности
Существующие схемы аппроксимации делятся на явные, когда все производные по координате в уравнении переноса записываются на «старом» (k– 1)-м временном слое с известным распределением переносимого параметра Т, и неявные, когда все производные по координате в этом уравнении записываются на «новом» k -м временном слое с неизвестным распределением Т. Используя формулу односторонней разности для производной по времени, а также формулу второй производной для диффузионного члена уравнения, запишем пример явной схемы аппроксимации:
Шаблон этой схемы, представляющий фрагмент сетки с минимальным количеством узловых точек, представлен на рис. 6.2.
Явная схема аппроксимации уравнения (6.36), заключающаяся в замене его левой части односторонней разностью, имеющей первый порядок точности, и записи правой части в конечных разностях на временном слое k– 1, где известно распределение параметра Т, позволяет получить явную формулу для температуры:
Вычисления по явной схеме первого порядка точности устойчивы, если коэффициент при Тi,k- 1оказывается положительным:
Это накладывает ограничение на выбор шага сетки по времени
Условие устойчивости явной схемы (6.40) является достаточно жестким. Так, при Hx= 0,01 м, а т=1,5×10–5 м2/c (сталь), N =20, шаг сетки по времени ht < 0,0083 c. Необходимость счета с мелким шагом по времени приводит к увеличению объема вычислений и является существенным недостатком, ограничивающим применение явной схемы первого порядка точности. От этого недостатка свободна неявная схема первого порядка точности, уравнение которой в соответствии с шаблоном на рис. 6.3 имеет вид
Согласно этой схеме правая часть уравнения (6.36) записывается на k -м временном слое с неизвестными значениями Т. Схема не дает явной формулы для определения неизвестных значений Т в узловых точках k -го слоя, а фиксирует лишь распределение:
где Соотношения (6.42) образуют для всех внутренних узловых точек k -го слоя систему линейных алгебраических уравнений (N– 1)-го порядка. Так как схема абсолютно устойчива, то счет можно вести с достаточно крупными шагами по времени. Это, однако, приводит к увеличению ошибок аппроксимации уравнения теплопроводности, поскольку соотношения между шагами сетки hx и ht, при котором ошибки аппроксимации левой и правой частей этого уравнения равны, имеет вид
Условие (6.43) показывает, что для обеспечения минимальной погрешности аппроксимации уравнения теплопроводности сгущение пространственной сетки в 2, 3, 4 раза должно вызывать соответствующее сгущение временной сетки в 4, 9, 16 раз.
|

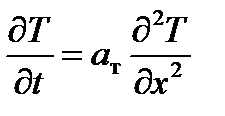 . (6.36)
. (6.36)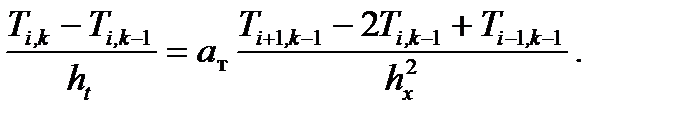 (6.37)
(6.37)
 . (6.38)
. (6.38)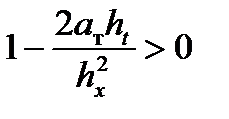 . (6.39)
. (6.39)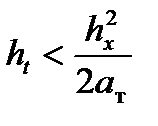 . (6.40)
. (6.40)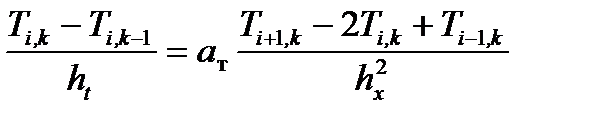 . (6.41)
. (6.41)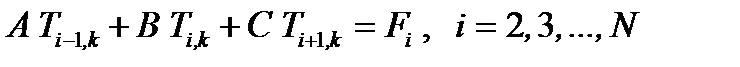 , (6.42)
, (6.42) .
.
 . (6.43)
. (6.43)


