Решение сеточных уравнений
Разностные уравнения, полученные из неявной схемы, являются, как было показано, линейными алгебраическими уравнениями. На фиксированном временном слое для всех внутренних узловых точек эти уравнения образуют систему
которую можно записать в векторно-матричном виде
или
где Матрица Одним из эффективных способов решения системы (6.44) является метод прогонки – модификация метода исключения Гаусса, учитывающая свойства матрицы H. В соответствии с методом прогонки решение системы (6.44) в узловой точке ищется в виде линейной функции. В частности, для (i−;1)-ой точки эта функция имеет вид
где
откуда находим
Полученное соотношение имеет ту же форму, что и функция (6.47), только для i -й точки
откуда заключаем, что
Полученные коэффициенты называются прогоночными коэффициентами, а формулы (6.50 – 6.51) дают процедуру решения методом прогонки. Сначала при i =2, 3,..., N считаются прогоночные коэффициенты (6.51), при этом начальные значения прогоночных коэффициентов Определение начальных значений прогоночных коэффициентов рассмотрим на примере граничных условий 1-го вида (изотермические границы). Пусть на левой и правой границах плоского слоя заданы следующие значения температур: Тi =1= T г1, Тi = N +1= T г2 . Тогда в соответствии с формулой (6.50) для левой границы
получаем начальные значения прогоночных коэффициентов
Таким образом, алгоритм метода прогонки имеет следующий вид:
Пример 6.2. В качестве теста для проверки алгоритма рассмотрим стационарную теплопроводность плоской стенки при граничных условиях первого рода. Решение задачи методом сеток дает систему уравнений с граничными условиями
При числе разбиений N =4, граничных условиях T г1=100, T г2=200 система имеет следующее решение: T 2=125, T 3=150, T 4=175. Запишем эту систему в векторно-матричной форме
алгоритм прогонки (6.54) реализуется для этой системы при A = C = 1, B = -2 следующим образом:
Основным недостатком метода прогонки являются ошибки округления при вычислении прогоночных коэффициентов. Эти ошибки возрастают с увеличением порядка системы. Для уменьшения этих ошибок рекомендуется считать эти коэффициенты с двойной точностью.
|

 , (6.44)
, (6.44) (6.45)
(6.45) , (6.46)
, (6.46)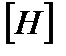 − матрица коэффициентов;
− матрица коэффициентов;  − вектор-столбец неизвестных значений искомого параметра Т в узловых точках;
− вектор-столбец неизвестных значений искомого параметра Т в узловых точках;  − неизвестный вектор столбец, характеризующий краевые условия и распределение параметра Т на предыдущем временном слое.
− неизвестный вектор столбец, характеризующий краевые условия и распределение параметра Т на предыдущем временном слое.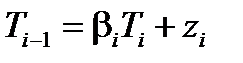 , (6.47)
, (6.47)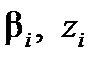 − неизвестные пока вспомогательные коэффициенты. Подставим (6.47) в (6.44):
− неизвестные пока вспомогательные коэффициенты. Подставим (6.47) в (6.44):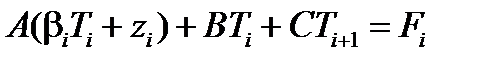 , (6.48)
, (6.48) . (6.49)
. (6.49)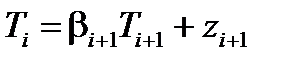 , (6.50)
, (6.50) (6.51)
(6.51)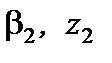 определяются из граничных условий на левой границе. Эта операция называется прямой прогонкой. После определения всех
определяются из граничных условий на левой границе. Эта операция называется прямой прогонкой. После определения всех  в обратном направлении (i = N, N−;1,..., 2) с учетом значения параметра
в обратном направлении (i = N, N−;1,..., 2) с учетом значения параметра 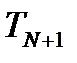 , найденного из граничного условия на правой границе, по формуле (6.50) последовательно находятся неизвестные значения
, найденного из граничного условия на правой границе, по формуле (6.50) последовательно находятся неизвестные значения  в узловых точках сетки.
в узловых точках сетки. , (6.52)
, (6.52)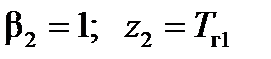 . (6.53)
. (6.53) ;
;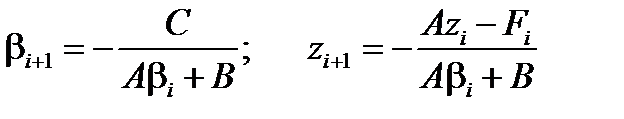 ,
, 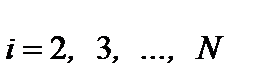 ; (6.54)
; (6.54)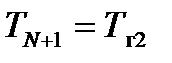 ;
; 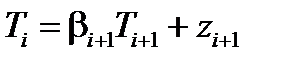 ,
, 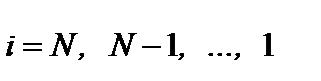 .
. . (6.55)
. (6.55)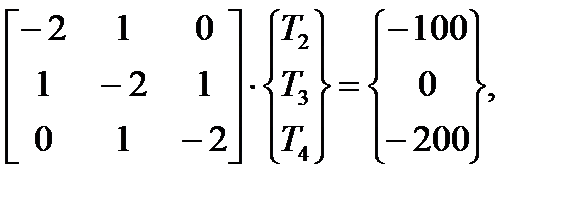
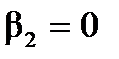 ;
;  ;
;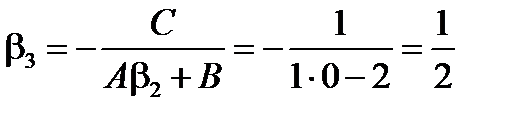 ;
;  ;
; ;
; 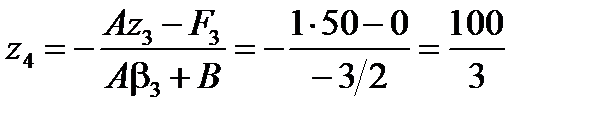 ;
; ;
; 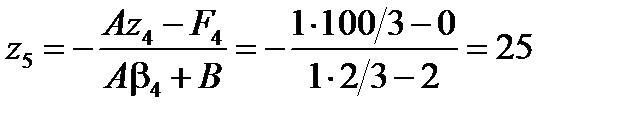 ;
;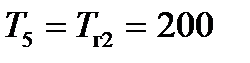 ;
;  ;
; 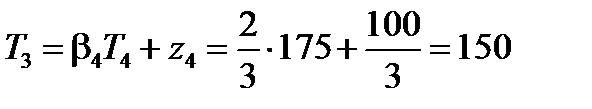 ;
;  ;
; 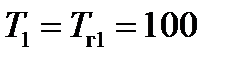 .
.


