Методические рекомендации по выполнению курсовой работы
Приведем пример структуры курсовой работы. Введениесодержит актуальность рассматриваемого вопроса, объект, цель и задачи исследования, методы исследования. 1. Характеристика дорожного движения на участке дороги. 1.1. Интенсивность движения. 1.1.1. Расчёт приведённой интенсивности движения по направлениям. 1.1.2. Построение пространственных картограмм интенсивности движения транспортных потоков в физических и приведённых единицах. 2. Оценка безопасности дорожного движения на перекрёстке. 2.1. Определение количества конфликтных точек и возможных конфликтных ситуаций. 2.1.1. Пофазная организация движения на перекрёстке. 2.1.2. Определение сложности и опасности перекрёстка. 3. Определение вида вероятностного распределения интервалов. 3.1. Расчёт фактических интервалов движения. 3.2. Построение гистограммы распределения интервалов. 4. Построение графиков зависимости между интенсивностью, плотностью и скоростью транспортных потоков. 4.1. Выбор скорости движения. 4.2. Модели Гринберга и Гриншилдса. 4.2. Расчёт интенсивности движения по моделям Гринберга и Гриншилдса. Заключение содержит оценку уровня загрузки перекрёстка, выводы по работе. Фактическую физическую интенсивность определяют для каждого из разрешённых направлений движения на перекрёстке (рис. 8.1) для каждого из рядов движения по каждому часу и в целом для всего перекрёстка.
Коэффициенты приведения для легковых автомобилей, грузовых автомобилей и автобусов, а также формулу для расчёта приведённой интенсивности необходимо определить по действующим нормативным документам. Число конфликтных точек определяется разрешёнными направлениями движения и количеством рядов движения транспортных средств. Надо учитывать также и пересечения траекторий движения транспортных средств и пешеходов. Необходимо в произвольном масштабе вычертить схему перекрёстка, указав на ней траектории разрешённых манёвров и ряды движения. По этой схеме следует определить число конфликтных точек различных типов, а затем рассчитать показатель сложности пересечения по пятибалльной системе оценки опасности конфликтных точек. По величине данного показателя надо отнести транспортный узел к одному из типов – простому, средней сложности и т.д. Затем необходимо с учётом интенсивности транспортных потоков и числа конфликтных точек рассчитать возможное число конфликтных ситуаций в час. Картограммы интенсивности движения транспортных потоков строятся по результатам расчётов физической и приведённой интенсивности. Для регулируемых перекрёстков необходимо: · составить схемы пофазной очерёдности движения (рис. 8.2) каждого регулируемого направления; ·
рассчитать длительности цикла, например:
где t з – время горения зелёного сигнала по соответствующему направлению; t 1 – время промежуточного такта (жёлтого сигнала), указывая длительности разрешающих тактов в фазах и переходные интервалы между фазами; · свести в таблицу длительности зелёного сигнала со стороны каждого направления. Для сравнительной оценки составленной организации движения на перекрёстке следует воспользоваться составлением показателей сложности т и опасности т' пересечений. Эти показатели зависят от числа полос, направления движения потоков и их интенсивностей. Показатель сложности пересечения m рассчитывается по числу точек соответственно отклонения, слияния и пересечения транспортных потоков по формуле (4.1). Так как возможность столкновений возрастает с увеличением интенсивности конфликтующих потоков, для оценки опасности вводятся индексы интенсивностей σ N (4.2), исходя из интенсивностей конфликтующих потоков в абсолютных (физических) единицах (авт./ч). Показатель опасности т' (4.3) рассчитывается как сумма условных баллов по числу конфликтных точек отклонений, слияний и пересечений на данном перекрёстке и соответствующим им индексам интенсивностей. Все конфликтные точки следует показать на картограммах и схемах пофазного проезда перекрёстка. Результаты расчётов m и m ´ сводятся в таблицу. Для каждого цикла регулирования определяются интервалы в течение каждого из заданных часов наблюдений по рядам движения. По каждому ряду продолжительности горения зелёного сигнала светофора принимается среднее значение интервала между следующими друг за другом автомобилями, делением на число зафиксированных проехавших автомобилей. Распределение интервалов времени между движущимися друг за другом автомобилями описывается вероятностными законами в зависимости от интенсивности транспортного потока и методов организации дорожного движения. Вся совокупность выборки интервалов в течение часа анализируется на предмет разбиения на группы разрядов расчётных интервалов. Графическая обработка результатов разбиения заключается в построении гистограммы распределения интервалов по экспериментальным данным (примерный её вид показан на рис. 8.3) и подбора её вида к одному из существующих распределений. Расчёт возможной пропускной способности каждой из полос движения и перекрёстка в целом проводится для интервала, соответствующего наибольшей вероятности по рис. 8.3. При этом принимается допущение одинаковости интервала в течение каждого часа наблюдений. Далее возможная пропускная способность сравнивается с установленной фактически.
Выбор скорости движения по каждой полосе в зависимости от величины наиболее часто встречающегося интервала производится по рис. 8.4 в следующей последовательности. 1. Строится основная диаграмма по основному уравнению транспортного потока
где q – интенсивность транспортного потока, авт./ч; k – плотность транспортного потока, авт./км; v – скорость, км/ч. При известных q цикли v циклиз формулы (8.2) выражаем:
где все значения принимаются за каждый цикл регулирования.
Основная диаграмма строится по точкам, полученным за каждый цикл (рис. 8.5). 2.
По построенной диаграмме определяется теоретическая пропускная способность как наибольшая интенсивность движения. Расчёт интенсивности движения по имитационным макромоделям Гриншильдса (8.4) и Гринберга (8.5)
где vf – скорость свободного движения, км/ч (принимается максимальная из зафиксированных за все часы наблюдения); k max– максимальная плотность потока, авт./км (выбирается по рис. 8.5).
где v max– скорость при максимальной интенсивности движения, км/ч (рассчитывается по формуле (8.5) при величине плотности, соответствующей теоретической пропускной способности из рис. 8.5). Построение остальных графиков зависимости между интенсивностью, плотностью и скоростью транспортных потоков (рис. 8.6).
Оценку уровня загрузки перекрёсткапроводят на основании оценок загрузки каждой полосы подхода к перекрёстку в отдельности. У каждого подхода свои пропускная способность, интенсивность и состав потоков. Требования по оформлению курсовой работы следующие. Ориентировочный объём работы 25-35 страниц. Ориентация листа – книжная. Титульный лист курсовой работы приведён в приложении 1. При компьютерном оформлении работы форматирование основного текста «по ширине», размер шрифта не более 14 пт, но не менее 12 пт, Times New Roman, межстрочный интервал – полуторный, поля, мм: 30 – левое; 10 – правое; 20 – верхнее; 20 – нижнее. При рукописном или компьютерном оформлении использовать черный или синий цвет. Все структурные элементы курсовой работы брошюруются (сшиваются) в следующей последовательности: · титульный лист; · задание кафедры на работу; · оглавление; · текст работы (включая введение, главы и заключение); · список использованных источников; · приложения (при необходимости). Список рекомендуемой литературы 1. Тарасик В.П. Теория автомобилей и двигателей: учеб. пособие / В.П. Тарасик, М.П. Бренч. – 2-е изд., испр. – Минск: Новое знание; М.: ИНФРА-М, 2013. – 448 с. 2. Бочкарев С.В., Цаплин А.И., Схиртладзе А.Г. Диагностика и надежность автоматизированных технологических систем: учеб. пособие / С.В. Бочкарев, А.И. Цаплин, А.Г. Схиртладзе. – Старый Оскол: ТНТ, 2013. – 616 с. 3. Цаплин А.И., Никулин И.Л. Моделирование теплофизических процессов и объектов в металлургии / А.И. Цаплин, И.Л. Никулин – Перм. гос. техн. ун-т. – Пермь, 2010. – 239 с. 4. Якимов М.Р. Транспортное планирование: создание транспортных моделей городов: монография / М.Р. Якимов. – М.: Логос, 2013. – 188 с.
8.3. Пример выполнения курсовой работы Введение. Транспортная инфраструктура – одна из важнейших инфраструктур, обеспечивающих жизнь городов и регионов. В последние десятилетия во многих крупных городах исчерпаны или близки к исчерпанию возможности экстенсивного развития транспортных сетей. Поэтому особую важность приобретает оптимальное планирование сетей, улучшение организации движения, оптимизация системы маршрутов общественного транспорта. Решение таких задач невозможно без математического моделирования транспортных сетей. Главная задача математических моделей – определение и прогноз всех параметров функционирования транспортной сети, таких, как интенсивность движения на всех элементах сети, объемы перевозок в сети общественного транспорта, средние скорости движения, задержки и потери времени и т.д. Математические модели, применяемые для анализа транспортных сетей, весьма разнообразны по решаемым задачам, математическому аппарату, используемым данным и степени детализации описания движения. Поэтому не представляется возможным дать исчерпывающую классификацию этих моделей. Основываясь на функциональной роли моделей, т.е. на тех задачах, для решения которых они применяются, можно условно выделить три основных класса моделей: · прогнозные; · имитационные; · оптимизационные. Прогнозные модели предназначены для решения следующей задачи. Пусть известны геометрия и характеристики транспортной сети, а также размещение потокообразующих объектов в городе. Необходимо определить, какими будут транспортные потоки в этой сети. В отличие от этого имитационное моделирование ставит своей целью воспроизведение всех деталей движения, включая развитие процесса во времени. При этом усредненные значения потоков и распределение по путям считаются известными и служат исходными данными для этих моделей. Кратко это отличие можно сформулировать так: прогнозные модели отвечают на вопрос: «сколько и куда» будут ехать в данной сети, а имитационные модели отвечают на вопрос: как в деталях будет происходить движение, если известно в среднем, «сколько и куда». Таким образом, прогноз потоков и имитационное моделирование являются дополняющими друг друга направлениями. Из сказанного следует, что к классу имитационных по их функциональной роли можно отнести широкий спектр моделей, известных под названием модели динамики транспортного потока. В моделях этого класса может применяться разная техника – от имитации движения каждого отдельного автомобиля до описания динамики функции плотности автомобилей на дороге. Для динамических моделей характерна значительно большая детализация описания движения и, соответственно, потребность в больших вычислительных ресурсах. Применение этих моделей позволяет оценить динамику скорости движения, задержки на перекрестках, длины и динамику образования «очередей» или «заторов» и другие характеристики движения. Основные области практического применения динамических имитационных моделей – улучшение организации движения, оптимизация светофорных циклов и др. В настоящее время актуальной задачей является разработка систем автоматизированного оперативного управления движением, работающих в режиме реального времени. Такие системы должны использовать информацию с датчиков в сочетании с динамическим имитационным моделированием. Однако помимо практических применений развитие динамических моделей представляет большой научный интерес в связи с изучением транспортного потока как физического явления со сложными и нетривиальными свойствами. Среди таких свойств – спонтанная потеря устойчивости, явления самоорганизации и коллективного поведения и др. Модели прогноза потоков и имитационные модели ставят своей целью адекватное воспроизведение транспортных потоков. Существует, однако, большое количество моделей, предназначенных для оптимизации функционирования транспортных сетей. В этом классе моделей решаются задачи оптимизации маршрутов пассажирских и грузовых перевозок, выработки оптимальной конфигурации сети и др. Методы оптимизации транспортных сетей представляют собой обширную область исследований, выходящую за рамки данного обзора. Характеристика дорожного движения на участке дороги включает: vf = 60 км/ч – скорость потока; v = 25 км/ч – скорость при повороте; q =1800 ед./ч – интенсивность транспортного потока (пропускная способность). Таблица 8.5
Таблица 8.6
Интенсивность движения – найдем приведенную интенсивность (таблица 8.7) движения по формуле:
где: q пр – приведенная интенсивность движения; qi – интенсивность движения транспортного потока в физическую единицу; pi – процентное содержание в потоке транспортных средств (табл. 8.7); K пр.л , K пр.г, K пр.а – коэффициенты приведения соответственно для легковых, грузовых автомобилей и автобусов. Таблица 8.7
Ниже даны пространственные картограммы интенсивности движения транспортных потоков в физических и приведенных единицах
Оценка безопасности дорожного движения на перекрестке включает определение количества конфликтных точек, возможных конфликтных ситуаций и пофазную организацию движения на перекрестке. Данный перекресток (рис. 8.8) имеет 32 конфликтные точки, из них 8 точек отклонения, 8 точек сложения и 16 точек пересечения. Исходя из этого, найдем показатель пересечения точек (m) и сложность перекрестка. Показатель пересечения точек и сложность перекрестка найдем по формуле:
где: n о – точка отклонения; n с – точка сложения; n п – точка пересечения.
Перекресток является сложным, т.к. значение m входит в промежуток для сложного перекрестка: - m <40 – перекресток с малым уровнем опасности; -40< m <80 – перекресток средней сложности; -80< m <150 – сложный перекресток; - m >150 – очень сложный перекресток. Потенциально опасная зона и условная конфликтная точка возникает между траекториями движения автомобиля, поворачивающего направо, и автомобиля, следующего за ним и намеревающегося двигаться по прямой. Конфликтная точка отклонения возникает, если маневрирующий автомобиль вынужден совершить задержку или выполнение поворота невозможно. В отличие от маневра отклонения слияние не возможно в любой момент времени, для этого необходимо, чтобы в потоке, с которым происходит слияние, образовался достаточный разрыв между транспортом. График режима работы светофора рассмотрим в соответствии с формулой для каждой фазы.
где: q – интенсивность транспортного потока (пропускная способность) дороги; qi – интенсивность транспортного потока полосы движения; n – число полос для движения; q пр – интенсивность прямого потока; q лев – интенсивность левого потока; q прав – интенсивность правого потока.
Таблица 8.8
Режим работы желтого сигнала:
где: t 1 – время проезда до стоп линии; t 2 – время проезда расстояния от стоп линии до контрольной точки; t 3 – время от момента включения зеленого сигнала до момента прибытия в конфликтной точке.
Длительность цикла:
Длительность основных циклов:
Таблица 8.9
Расчёт фактического интервала движения между автомобилями описывается вероятностными законами в зависимости от интенсивности транспортного потока и методов организации дорожного движения. Вся совокупность выборки интервалов в течение часа анализируется на предмет разбиения на группы разрядов расчётных интервалов. Выбор наиболее часто встречающегося интервала для каждого часа:
где: n – количество циклов, t ц – время цикла.
Таблица 8.10
Фактический интервал движения:
где: t зел – время зеленого сигнала; N – время приведенного интервала. Шаг интервала:
где: t max – максимальное время интервала; t min – минимальное время интервалов. h =0,546 Вариационный ряд: 0,063; 0,085; 0,094; 0,127; 0,127; 0,127; 0,141; 0,141; 0,141; 0,141; 0,157; 0,159; 0,159; 0,159; 0,170; 0,177; 0,177; 0,177; 0,182; 0,182; 0,189; 0,202; 0,202; 0,7
Рис. 8.9. Вероятностная гистограмма распределений
Расчёт интенсивности движения по имитационным макромоделям – моделям Гринберга, Гриншилдса. Основное уравнение транспортного потока:
где: q – интенсивность транспортного потока; k ц – плотность цикла; v – скорость цикла. Таблица 8.11
Графики зависимости между интенсивностью, плотностью и скоростью транспортных потоков представлены на рис. 8.10 – 8.12.
Модель Гриншилдса (8.5):
где: q – интенсивность потока; vf – скорость свободного движения; k max – максимальная плотность потока, (k max=9,2 авт./км). Модель Гринберга (8.4):
Таблица 8.12. Результаты реализации моделей Гринберга и Гриншилдса
Вывод: курсовая работа по моделированию дорожного движения помогает исследовать характеристику транспортного потока, статистически обрабатывать результаты измерений и дает оценку уровня загрузки перекрестка. Применение методов обработки экспериментальных данных об измерениях интенсивности и интервалов между автомобилями в транспортном потоке на регулируемом перекрестке дает план теоретической зависимости и построения имитационных моделей. Основной задачей было определение стохастического характера поступления на перекресток, оценка уровня пропускной способности на примере реального перекрестка.
|

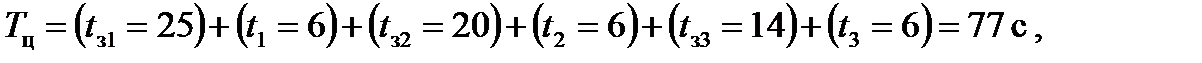 (8.1)
(8.1)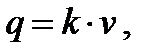 (8.2)
(8.2)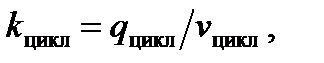 (8.3)
(8.3)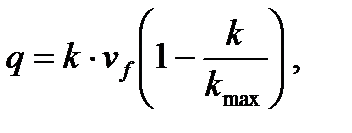 (8.4)
(8.4)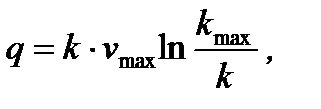 (8.5)
(8.5) (8.6)
(8.6)



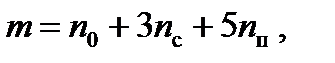 (8.7)
(8.7)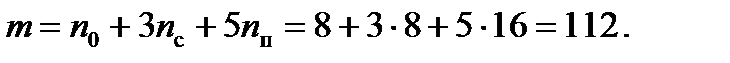


 (8.8)
(8.8)
 (8.9)
(8.9)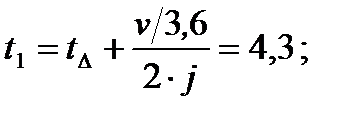 (8.10)
(8.10) (8.11)
(8.11) (8.12)
(8.12)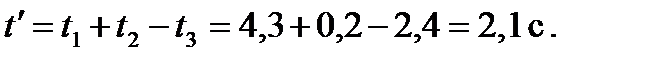
 (8.13)
(8.13)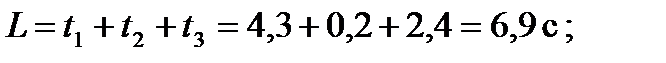 (8.14)
(8.14) T=37,7;
T=37,7;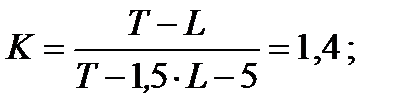 (8.15)
(8.15)
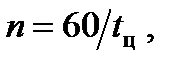 (8.16)
(8.16) (8.17)
(8.17)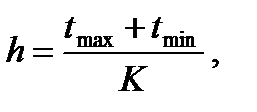 (8.18)
(8.18)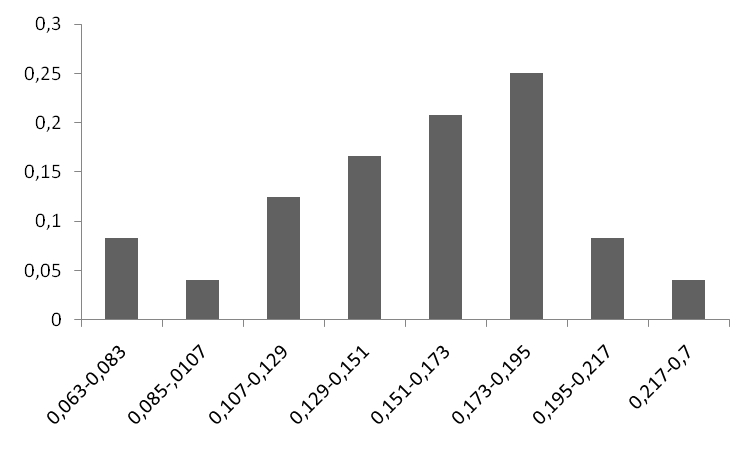
 (8.19)
(8.19)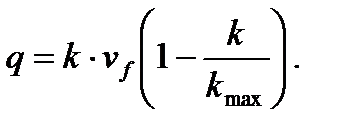 (8.20)
(8.20) (8.21)
(8.21)


