Числоопорных витков
число срезанных витков длина пружины в свободном состоянии действующее на пружину усилие предварительного сжатия рабочее осевое усилие Выносливость пружины не более предел прочности модуль упругости коэффициент Пуассона модуль сдвига плотность Расчет Припроверочном расчете по заданным внешним геометрическим размерам нужно определить коэффициент запаса статической прочности, а в случае действия переменной нагрузки — и коэффициент усталостной прочности. Начинать следует с нахождения основных параметров пружины: индекс, осадка, длина, шаг и т. д. Индекс пружины
Осадка пружины зависит от действующих на нее сил. Если пружина эксплуатируется в режиме переменного нагружения, то в качестве сил, действующих на нее в процессе работы, можно рассматривать максимальную и минимальную силы, т. е. в данном случае
222 Глава 4. Типовые элементы машин
Наименьшая осадка пружины (при минимальной силе): Полное число витков с учетом опорных:
Длина пружины в полностью сжатом состоянии:
Шаг пружины в нагруженном состоянии: 4.4. Расчет упругих элементов машин 223 Для того чтобы перейти к определению критической скоростинужно вычислить вспомогательный коэффициент
Тогда критическая скорость равна
Далее находим коэффициенты запаса. Допускаемое напряжение сдвига: (пружина первого класса).
Фактическое напряжение сдвига:
Коэффициент запаса статической прочности:
Максимальное напряжение цикла:
Минимальное напряжение цикла:
Среднее напряжение цикла:
224 Глава 4. Типовые элементы машин Амплитудное напряжение цикла:
Коэффициент запаса усталостной прочности (2.10.20):
где
коэффициент асимметрии цикла.
Примем В заключение проверим пружины на устойчивость. Пружина считается устойчивой, если Если условие устойчивости пружины оказывается не выполненным, тогда для ее нормальной эксплуатации необходимо дополнительно использовать оправку.
|



 Характеристики материала пружинной проволоки:
Характеристики материала пружинной проволоки: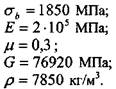
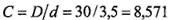
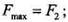
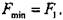
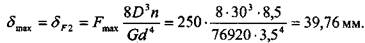




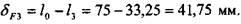

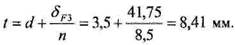
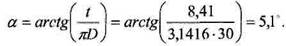


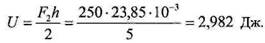
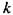 , а также рассчитать силу
, а также рассчитать силу 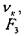 и напряжение сдвига
и напряжение сдвига  при полном сжатии:
при полном сжатии: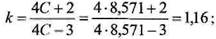
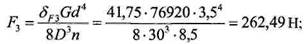

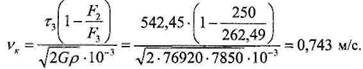
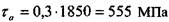
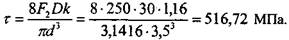

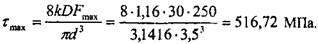


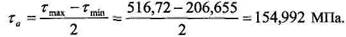

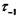 — предел выносливости, вычисляемый как
— предел выносливости, вычисляемый как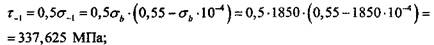
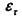 — масштабный фактор (для проволоки диаметром менее 10 мм принимается равным единице);
— масштабный фактор (для проволоки диаметром менее 10 мм принимается равным единице);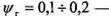

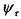 =
= 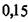 , тогда
, тогда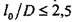 . В нашем случае 75/30 = 2,5, следовательно, пружина устойчива.
. В нашем случае 75/30 = 2,5, следовательно, пружина устойчива.


