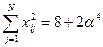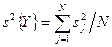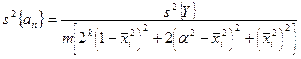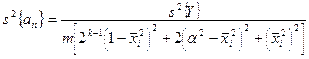Обработка и анализ результатов для ЦКОП.
Для ЦКОП обработка и анализ результатов проводится аналогично ПФЭ, в той же последовательности и с использованием тех же формул для оценки дисперсий среднего арифметического и адекватности. Исключение составляют формулы для расчета коэффициентов полинома и дисперсии их определения. В силу ортогональности матрицы ЦКОП все коэффициенты имитационной модели в виде полинома второго порядка определяются, как и для ПФЭ, независимо друг от друга. Но если при подсчете коэффициентов в знаменателе используется одно и тоже значение N (числа опытов), то в ЦКОП расчет коэффициентов полинома ведется по формуле
Это означает, что при определении коэффициентов полинома значение знаменателя для различных групп коэффициентов будет различным. Так, для не преобразованной матрицы для а 0 знаменатель будет
для группы коэффициентов при линейных членах xi полинома
для группы коэффициентов xixj или x 1 x 2 x 3, учитывающих взаимодействие факторов,
для коэффициентов при квадратичных членах
Соответственно формула для расчета дисперсии коэффициентов полинома, будет иметь вид
Расчет дисперсии воспроизводимости эксперимента s 2{ Y } при оценки дисперсии коэффициентов производится по обычной формуле
Из сравнения формул для оценки дисперсий коэффициентов в случае ПФЭ и ЦКОП видно, что дисперсия будет различной для различных групп коэффициентов. Для непреобразованной матрицы оценку для всех групп коэффициентов легко получить, учитывая приведенные выше значения знаменателя. Для приведенной матрицы ЦКОП в соответствии с табл. … оценка дисперсии различных коэффициентов в общем виде может быть представлена, как
При k<5, когда ЦКОП базируется на ПФЭ типа 2 k
где При k ≥5, когда ЦКОП базируется на ДФЭ типа 2 k -1,
Согласно приведенным формулам значение t -параметра, будет отличаться знаменателем для различных групп коэффициентов полинома. А это означает, что в отличии от линейного приближения, при ортогональном планировании на базе полинома второго порядка оценка значимости найденных коэффициентов полинома ЦКОП будет проводиться с различной точностью и изменяться с поворотом координат. Изменение дисперсии ошибок определения коэффициентов полинома при повороте координат приводит к тому, что в ЦКОП точность предсказания выходной величины (значения функции отклика) в различных направлениях факторного пространства различна. Это означает, что точность определения математической модели исследуемого процесса (её конкретный вид зависит от точности определения коэффициентов полинома) во всех направлениях факторного пространства не одинакова. Различие в точности оценок коэффициентов полинома при описании областей, близких к экстремуму, особенно нежелательно, так как исследователю при планировании экстремальных экспериментов необходимо иметь высокую точность описания процесса именно в этих областях. В этом случае более удачным является ЦКРП, который позволяет обеспечить практически одинаковую точность определения функции отклика во всех направления факторного пространства на одинаковом расстоянии R от центра планирования.
|

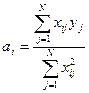

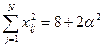

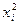 полинома
полинома