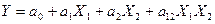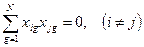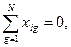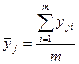Полный факторный эксперимент

В этом случае учитывается влияние на функцию отклика исследуемого процесса не только каждого рассматриваемого в эксперименте фактора в отдельности, но и их взаимодействий.

Под взаимодействием факторов понимают эффект влияния изменения значений одного или нескольких факторов на характер изменения функции отклика Y от изменения другого фактора. Влияние взаимодействия факторов – это когда уровень одного фактора определяет характер влияния другого фактора на выходной параметр.

 

На рисунке 10 а) видно, что переход фактора X₁ с одного уровня 400˚С на другой 450˚С не меняет характер влияния второго фактора на Y; в этом случае взаимодействие факторов X₁X₂ не оказывает влияние на функцию отклика. На другом рис. 10 б) изменение уровня фактора X₁ сказывается на наклоне линейной зависимости Y (X₂), что говорит о влиянии взаимодействия факторов X₁X₂ на выходной параметр Y.

При построении матрицы полного факторного эксперимента (ПФЭ), допустим, что в исследуемом процессе участвуют только два фактора X₁ и X₂, оказывающие влияние на интересующую нас функцию отклика.

В соответствии с принципом «от простого к более сложному» предположим, что модель исследуемого процесса является линейной и описывается полиномом первого порядка:

где a ₀ – значение функции отклика Y в центре плана; коэффициент a_i характеризует степень влияния i -ого фактора на функцию отклика Y (чем он больше по сравнению с другими коэффициентами, тем более весомый вклад в изменение Y данный фактор вносит); член a ₁₂X₁X₂ учитывает эффект влияния взаимодействия 1-ого и 2-ого факторов на функцию отклика, a ₁₂ характеризует весомость этого влияния.

Вполне очевидно, варьирование значений фактора относительного его базового значения в случае линейной модели достаточно проводить только на двух уровнях.

Легко видеть, что все возможные комбинации для двух факторов, варьируемы на двух уровнях, будут исчерпаны, если поставить всего четыре опыта. Опытные точки расположатся в вершинах квадрата, центр которого совпадает с центром плана.

Как видно, каждому из этих четырех опытов будет соответствовать свое значение функции отклика, в зависимости от четырех различных сочетаний двух значений варьируемых в данном эксперименте факторов.

Построим матрицу планирования ПФЭ для рассматриваемого случая, с учетом предполагаемой модели исследуемого процесса.

При построении матрицы планирования ПФЭ существует следующее правило:

Первая строка матрицы в столбцах, соответствующим рассматриваемым в эксперименте факторам, заполняется безразмерным символом, соответствующим нижнему уровню значений фактора в эксперименте (–); продолжение заполнения столбца, соответствующего первому по порядку фактору, проводится последовательным чередованием противоположных знаков; все последующие столбцы, соответствующие другим пронумерованным по порядку факторам, заполняются с частотой смены знака вдвое меньшей, чем для предыдущего столбца. Заполнение столбцов, учитывающих взаимодействие факторов, производится как результат перемножения знаков соответствующих факторов в каждой строке.

Первый столбец матрицы представляет собой нумерацию опытов. Во втором заносятся значения фиктивного фактора X₀, соответствующего коэффициенту a ₀, и принимающего значения +1. В последующих столбцах матрицы приводятся безразмерные значения, соответствующие верхнему и нижнему уровням варьирования факторов и их взаимодействий. В последний столбец матрицы заносятся экспериментальные значения функции отклика, полученные в результате проведения каждого опыта.

Так как в полученной матрице рассматриваются два фактора на двух уровнях, то подобную матрицу планирования ПФЭ называют 2²

Матрица планирования должна отвечать следующим условиям:

1. Для обеспечения независимости оценки коэффициентов полинома необходимо соблюдение независимости столбцов матрицы планирования эксперимента, или, иначе говоря, построенная матрица планирования должна быть ортогональной. Матрица планирования эксперимента является ортогональной, если сумма произведений значений, приведенных в каждой строке двух любых столбцов матрицы, равна нулю.

2. Условие нормированости

3. Симметричность относительно центра экстремума

4. Ротатабельность, т.е. координаты точек факторного пространства в матрице планирования подстраиваются так, что точность предсказания значения параметра оптимизации одинакова на равных расстояниях от центра эксперимента (базовой точки) и не зависит от направления.

 

Номер опыта	x 0	x 1	x 2	x 1 x 2	y
	+	–	–	+	y 1
	+	+	–	–	y 2
	+	–	+	–	y 3
	+	+	+	+	y 4

 

Одним из важнейших положений современной теории планирования эксперимента является рандомизация. План эксперимента составляется так, чтобы рандомизировать, т.е. сделать случайными те систематически действующие факторы, которые трудно поддаются учету и контролю, для того, чтобы рассматривать их как случайные величины и учитывать статистически.

Перед реализацией плана на объекте необходимо произвести рандомизацию - с помощью таблицы равномерно распределенных случайных чисел (см. Табл. 1. Приложение) определить последовательность реализации матрицы планирования в каждой из m серий опытов.

После выполнения ПФЭ осуществляют независимую оценку коэффициентов полинома по следующей формуле:

В числителе фактически стоит сумма средних значений выходного параметра по всем опытам с учетом уровня независи­мой переменной x_i в j -м опыте.

Следует отметить, что здесь мы можем найти так­же коэффициенты a_ij при произведениях факторов x_ix_j (i ≠ j). Значения этих коэффициентов показывают уровень влияния эф­фекта взаимодействия факторов x_i и x_j.

Если в эксперименте используются три фактора, а предполагаемая математическая модель линейна, то она соответствует полиному вида:

При варьировании каждым из трёх факторов на двух уровнях число опытов будет составлять N =2³=8, а матрица планирования ПФЭ будет иметь следующий вид.

Таблица. 1
Номер опыта	x 0	x 1	x 2	x 3	x 1 x 2	x 2 x 3	x 1 x 3	x 1 x 2 x 3	y
	+	–	–	–	+	+	+	–	y 1
	+	+	–	–	–	+	–	+	y 2
	+	–	+	–	–	–	+	+	y 3
	+	+	+	–	+	–	–	–	y 4
	+	–	–	+	+	–	–	+	y 5
	+	+	–	+	–	–	+	–	y 6
	+	–	+	+	–	+	–	–	y 7
	+	+	+	+	+	+	+	+	y 8

 

В этом случае точки располагаются в вершинах куба, центр которого находится в начале координат.

Руководствуясь приведенным выше правилом, легко построить матрицу и для большего числа рассматриваемых факторов, число опытов в которой

N =2 ^k

где k – число учитываемых в эксперименте факторов.

Однако следует подчеркнуть, что данное выражение справедливо только для линейной модели, соответствующей полиному 1-ого порядка, когда варьирование по каждому фактору достаточно проводить на двух уровнях.

При статистическом методе планирования эксперимента существует правило – число уровней варьирования, учитываемых в эксперименте факторов, должно быть, по крайней мере, на единицу больше порядка полинома, для построения которого планируется эксперимент.

Если анализ результатов эксперимента показывает, что линейная модель, соответствующая полиному первого порядка, не адекватна исследуемому процессу, то переходят к планированию и проведению следующего эксперимента исходя из предположения, что математическая модель соответствует полиному следующего порядка и так далее. Но при планировании эксперимента, основанного на математической модели, соответствующей полиному 2-ого порядка

необходимо обеспечить варьирование по каждому из n факторов уже на трёх уровнях. А тогда необходимое число опытов, которое нужно провести в эксперименте, должно быть не меньше N = 3 ^k. Для полинома третьего порядка N = 4 ^k и так далее.

Отметим некоторые положительные особенности многофакторного планирования ПФЭ.

1. Опытные точки находятся в оптимальном положении, то есть математическое описание исследуемого процесса оказывается более точным, чем при проведении опытов в точках, расположенных каким-либо другим образом.

2. Планирование и проведение ПФЭ сравнительно просто, что объясняет его широкое применение на практике.

3. Все факторы и соответственно коэффициенты полинома оцениваются независимо друг от друга, что обеспечивается независимостью и ортогональностью столбцов матрицы планирования.

Однако последняя положительная особенность ПФЭ справедлива только для процесса, описываемого полиномом первого порядка. При значительном влиянии на выходной параметр уже квадратичных членов полинома, оценивать раздельно коэффициенты полинома с помощью ПФЭ, как правило, не удается, так как соответствующие столбцы матрицы планирования будут идентичны между собой и, следовательно, матрица становится неортогональной, то есть с зависимыми столбцами.

Проведение эксперимента. Оно должно обеспечить сведение к минимуму влияние случайных (неконтролируемых) параметров исследуемого процесса на функцию отклика.

С целью уменьшения этого влияния на конечный результат эксперимента, необходимо придерживаться следующих требований.

Во-первых, предусмотреть проведение нескольких параллельных опытов при одних и тех же условиях, предусмотренных соответствующей строкой матрицы планирования.

Во-вторых, необходимо рандомизировать неконтролируемые параметры процесса, то есть обеспечить их взаимную компенсацию.

Для выполнения первого требования необходимо предусмотреть проведение не менее двух параллельных опытов, а для более высокой достоверности результатов, их число увеличивают. В этом случае результаты m параллельных опытов усредняются и при анализе результатов эксперимента используют именно усредненное значение функции отклика, соответствующие условиям опыта и подсчитываемое по формуле

где j – номер опыта по порядку; i – номер параллельного опыта в строке; y_ji – значение функции отклика, соответствующее i -му параллельному опыту в j -ой строке матрицы планирования; m – число параллельных опытов.