Моделирование методом кусочно-линейной аппроксимации, разветвляющиеся и циклические алгоритмы.

Метод кусочно-линейной аппроксимации заключается в замене заданной нелинейной характеристики ломаной прямой с одной или несколькими точками излома. Такая замена нелинейной характеристики позволяет вести расчет аналитически с помощью линейных уравнений. Для прямолинейных участков записываются линейные уравнения, решения которых припасовываются: электрические величины для конца участка приравниваются соответствующим величинам для начала следующего участка.

 

Линейный алгоритм – описание действий, которые выполняются однократно в заданном порядке. Исполнитель выполняет действия последовательно, одно за другим в том порядке в котором они следуют.

Циклический алгоритм – описание действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие. Перечень повторяющихся действий называют телом цикла.

Циклические алгоритмы бывают двух типов:

А. Циклы со счетчиком, в которых какие-то действия выполняются определенное число раз;

Б. Циклы с условием, в которых тело цикла выполняется, в зависимости от какого-либо условия. Различают циклы с предусловием и постусловием.

Разветвляющийся алгоритм – требуется, чтобы при одних условиях выполнялась одна последовательность действий, а при других – другая.

Условие – это высказывание, которое может быть либо истинно, либо ложно.

Системы счисления. Позиционная и непозиционная системы счисления. Перевод чисел из одной системы счисления в другую. Перевод десятичных чисел в двоичную, восьмеричную и шестнадцатеричную. Перевод десятичных дробей.

Система счисления – способ записи чисел с помощью последовательности цифр, символов, имеющие определенное значение. В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. В позиционной системе счисления количественное значение зависит от ее места или позиции в числе. Основание систем счисления – количество P различных цифр, используемых для записи числа в позиционной системе. Значение цифр изменяется от нуля до P-1. 1. Двоичная. Используются только 2 цифры: 0 и 1. 2. Восьмеричная. В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления. 3. Шестнадцатеричная. В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв.

Перевод чисел из одной системы в другую. 2 → 8, триадами. 2 → 16, тетрадами. Любое число → 10, степенью основания. 10 → любое число, делением. Перевод десятичных дробей: 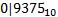· 8 = 7|5000 · 8 = . Ответ: 0,75.