Свойства. · Инвариантность ранга при элементарных преобразованиях
· Инвариантность ранга при элементарных преобразованиях Теорема (об инвариантности ранга при элементарных преобразованиях) Если
· Эквивалентность СЛАУ при элементарных преобразованиях Назовём элементарными преобразованиями над системой линейных алгебраических уравнений: перестановку уравнений; умножение уравнения на ненулевую константу; сложение одного уравнения с другим, умноженным на некоторую константу. Т.е. элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:
Теорема (об эквивалентности систем уравнений при элементарных преобразованиях). Система линейных алгебраических уравнений, полученная путём элементарных преобразований над исходной системой, эквивалентна ей
· Нахождение обратных матриц Теорема (о нахождении обратной матрицы). Пусть определитель матрицы
· Приведение матриц к ступенчатому виду Введём понятие ступенчатых матриц:
Матрица Все нулевые строки матрицы Для любой ненулевой строки матрицы
Тогда справедливо следующее утверждение: Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду.
Эквивалентные матрицы
Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.
Надо отметить, что равные матрицы и эвивалентные матрицы - понятия совершенно различные.
Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк.
Т.к. элементарные преобразования не изменяют ранг матрицы, то можно существенно упростить процесс нахождения ранга матрицы.
5. Блочная (клеточная) матрица — вид квадратной матрицы, каждый элемент которой является квадратной подматрицей меньшей, кратной размерности.
Пример записи Матрица размерностью 4×4
является блочной, состоящей из четырех подматриц-блоков размерностью 2×2
Если каждый блок будет определен как
то, блочная матрица может быть записана в следующем виде
|

 , то
, то 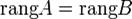
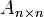 не равен нулю, пусть матрица
не равен нулю, пусть матрица 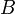 определяется выражением
определяется выражением 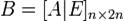 . Тогда при элементарном преобразовании строк матрицы
. Тогда при элементарном преобразовании строк матрицы 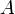 к единичной матрице
к единичной матрице  в составе
в составе 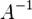
 ) справедливо следующее: если
) справедливо следующее: если  — первый ненулевой элемент строки
— первый ненулевой элемент строки  .
.





