Свойства обратной матрицы
Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A − 1 существует, то x = A − 1b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
15. Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы. Пусть Тогда по определению рангом матрицы A является: · ноль, если A — нулевая матрица; · число Теорема (о корректности определения рангов). Пусть все миноры матрицы
16. Строчнопсевдотреугольная – если в каждой нулевой строке найдется хотябы один нулевой элемент, в столбце которого все нижележащие елементы (если они есть) = 0
Строчнопсевдодиагональная – если в каждой нулевой строке найдется хотябы один нулевой елемент, в столбце которого строго все елементы лежащие выше (если они есть) = 0
17. Линейное пространство. Основные понятия Пусть
паре элементов множества
паре
Будем называть множество
существует единственный нулевой элемент для каждого элемента существует единственный противоположный элемент
Равенства 1--8 называют аксиомами линейного пространства.
Линейное пространство часто называют векторным пространством, а его элементы – векторам
18. РАЗМЕРНОСТЬ ЛИЕЙНОГО ПРОСТРАНСТВА Число k называется размерностью линейного пространства L, если в L существует система из k линейно независимых векторов, а любая система из k+1 вектора — линейно зависима. Обозначается dimL = k. Пространство L называется k- мерным. Иногда обозначается Lk. Векторы i и j — линейно независимая система векторов линейного пространства геометрических радиусов-векторов плоскости R2.
Рассмотрим произвольную систему из трёх векторов x, y, z.
На рисунке показано, что вектор z линейно выражается через векторы x и y: z = α1·x + α2·y.
Итак, в пространстве R2 существует система из двух линейно независимых векторов (i, j), а любые три вектора образуют линейно зависимую систему. То есть размерность пространства R2 равна 2, dim R2 = 2.
19. Изоморфи́зм — это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.
Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными», они называются изоморфными. Классическим примером изоморфных систем могут служить множество
20.
|

 , где
, где 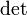 обозначает определитель.
обозначает определитель.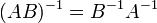 для любых двух обратимых матриц A и B.
для любых двух обратимых матриц A и B. где * T обозначает транспонированную матрицу.
где * T обозначает транспонированную матрицу. для любого коэффициента
для любого коэффициента 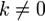 .
.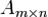 — прямоугольная матрица.
— прямоугольная матрица. , где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
, где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.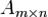 порядка k равны нулю (Mk = 0). Тогда
порядка k равны нулю (Mk = 0). Тогда 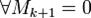 , если они существую
, если они существую множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:
множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число: ,
, 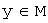 отвечает элемент
отвечает элемент  , называемый суммой
, называемый суммой 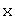 и
и  ;
; отвечает элемент
отвечает элемент 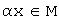 , называемый произведением числа
, называемый произведением числа  и элемента
и элемента 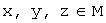 и произвольных чисел
и произвольных чисел 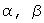 справедливо:
справедливо: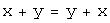 , сложение коммутативно;
, сложение коммутативно; , сложение ассоциативно;
, сложение ассоциативно; такой, что
такой, что 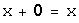 ,
, 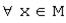 ;
;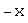 такой, что
такой, что 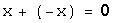 ,
,  , умножение на число ассоциативно;
, умножение на число ассоциативно;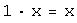 ;
;  , умножение на число дистрибутивно относительно сложения элементов;
, умножение на число дистрибутивно относительно сложения элементов; , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел.
 всех вещественных чисел с определённой на нём операцией сложения и множество
всех вещественных чисел с определённой на нём операцией сложения и множество 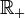 положительных вещественных чисел с заданной на нём операцией умножения. Отображение
положительных вещественных чисел с заданной на нём операцией умножения. Отображение 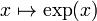 в этом случае является изоморфизмом.
в этом случае является изоморфизмом.


