Горизонтальный и вертикальный кругиГоризонтальный угломерный круг представляет собой два стеклянных круга, расположенных соосно. На нижнем круге, называемом лимбом, нанесена круговая шкала с делениями через 1° по часовой стрелке от 0° до 359°; таким образом, цена деления лимба составляет1°. Верхний круг - алидада - содержит дугу окружности в 1°, разделенную на 12 частей; следовательно, цена деления алидады составляет 5¢. Для отсчитывания по угломерным кругам используется шкаловой микроскоп, в поле зрения которого передается изображение делений на алидаде и примыкающих к ним делений на лимбе (рис. 3.4). Отсчитывание по горизонтальному кругу выполняется на глаз с точностью 1/10 цены деления алидады, то есть с точностью 0.5'.
Рис. 3.4. Поле зрения микроскопа
Вертикальный круг отличается от горизонтального тем, что его лимб скреплен со зрительной трубой и вращается вместе с ней, а алидада неподвижна, деления на нем нанесены от 0 в положительном и отрицательном направлениях. Место нуля (обозначается как МО) – отсчет по вертикальному кругу, когда визирная ось занимает горизонтальное положение и пузырек цилиндрического уровня находится в нуль-пункте. Порядок отсчитывания по угломерным кругам. Для взятия отсчетов по горизонтальному кругу служит нижняя шкала в поле зрения микроскопа (отмечена буквой Г), для отсчетов по вертикальному кругу – верхняя шкала (отмечена буквой В). При отсчитывании по горизонтальному кругу число градусов равно числу градусов того штриха на лимбе, который попал на шкалу, а число минут на алидаде отсчитывается от нуля до этого градусного деления (слева направо). Отсчеты берутся с точностью 0.5¢. Так, на рис. 3.4 справа отсчет равен 124° 42.0¢. Отсчет по вертикальному кругу может быть положительным и отрицательным. Если число градусов положительно, то отсчет берется так же, как и по горизонтальному кругу. Если число градусов со знаком “минус”, то число минут отсчитывается справа налево. На рис. 3.4. отсчет по вертикальному кругу равен -2° 47.5¢ (в данном случае минуты отсчитываются справа налево). Может возникнуть вопрос: “Почему не разбит каждый градус на лимбе?” Тогда на алидаде было бы достаточно одного штриха и считывание отсчетов было бы более простым. Ответ состоит в следующем. Если точность измерения углов составляет 30", то деления на лимбе должны быть нанесены на порядок точнее, чтобы сделать неощутимым влияние ошибок их положения. Для теодолита 2Т30 угловая ошибка делений лимба не должна превышать величину порядка 3". Если принять радиус лимба 100 мм, то линейная ошибка делений лимба не должна превышать
Следовательно, каждое деление на лимбе нанесено с ошибкой не более 1.5 мкм. Нанесение делений с такой точностью требует существенных затрат времени работы делительной машины. Если бы на лимбе наносили деления через каждые 5', то общее число делений было бы в 12 раз больше и соответствующим образом возросло бы время для их нанесения. Таким образом, разбиение всего одного градусного деления на алидаде на 12 частей незначительно усложняет порядок взятия отсчетов по угломерным кругам, но существенно сокращает затраты времени на их изготовление.
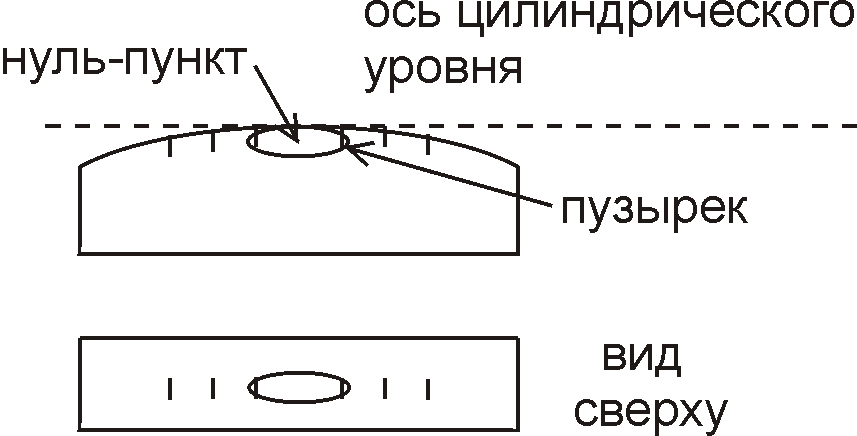
Уровни Цилиндрический уровень представляет собой стеклянную ампулу цилиндрической формы, внутренняя поверхность которой в вертикальной плоскости является дугой окружности большого радиуса (рис. 3.5). Ампула запаивается с одного конца, в нее заливается подогретый спирт или эфир, после чего запаивается другой конец ампулы. При остывании жидкости образуется безвоздушное пространство, которое называют пузырьком цилиндрического уровня.
Рис. 3.5. Цилиндрический уровень
Сверху ампулы наносится шкала с делениями через 2 мм. Среднее деление этой шкалы называют нуль-пунктом. Ось цилиндрического уровня - прямая, касательная к внутренней поверхности ампулы в нуль-пункте. Точность цилиндрического уровня характеризует цена деления уровня - центральный угол, опирающийся на дугу окружности, равную одному делению. Чем больше радиус указанной окружности, тем выше чувствительность уровня: при наклонах уровня наблюдается перемещение его пузырька. Цена деления у различных теодолитов составляет от 10² до 60², у теодолита 2Т30 она равна 45². Из формулы
где R – радиус окружности, d =2 мм - длина дуги окружности и
|
.
,
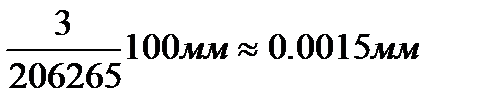– центральный угол, выраженный в радианах, 206265 – число секунд в радиане, следует, что радиус дуги окружности цилиндрического уровня составляет величину порядка
