Принцип измерения углов

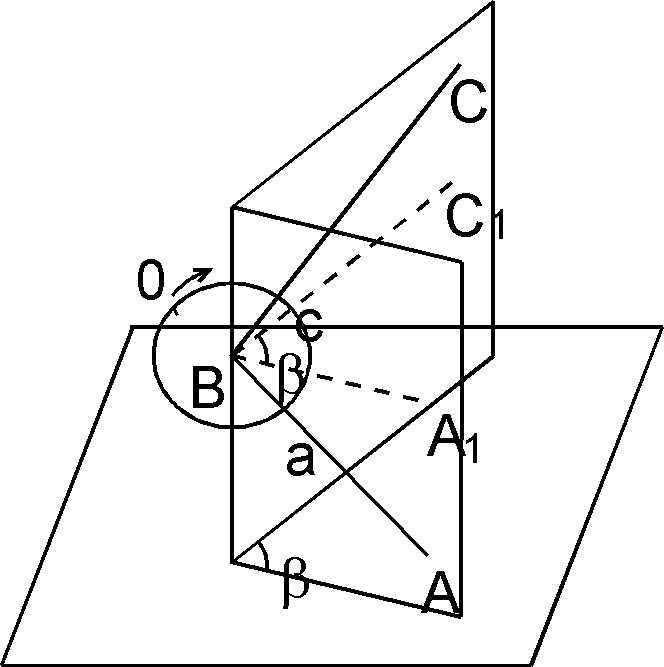
По указанным выше причинам в геодезии принято измерять, как правило, не произвольные, а горизонтальные и вертикальные углы. Горизонтальный угол – это плоский угол, образованный проекциями точек местности на горизонтальную плоскость. Аналогичное определение дает ГОСТ 22268 “Горизонтальный угол – двугранный угол, ребро которого образовано отвесной линией, проходящей через данную точку”. Вертикальный угол некоторой линии – это угол между данной линией и горизонтальной плоскостью. Для их измерения используются горизонтальные и вертикальные круги с делениями, называемые угломерными кругами.

Измерение горизонтального угла (пусть это будет угол ABC на рис. 3.1) в принципе выполняется следующим образом.

1) Центр угломерного круга располагается на отвесной линии, проходящей через вершину угла B.

2) Угломерный круг приводится в горизонтальное положение (отвесная линия при этом будет совпадать с нормалью к плоскости угломерного круга).

3) Через вершину B и правую точку A измеряемого угла проводится вертикальная плоскость. При ее пересечении со шкалой угломерного круга получим отсчет a.

4) Через вершину B и левую точку С измеряемого угла проводится вертикальная плоскость. Ее пересечение со шкалой угломерного круга даст отсчет c.

5) Если деления на угломерном круге нанесены по часовой стрелке, то горизонтальный угол b будет равен разности отсчетов по горизонтальному кругу

.

 

 

Рис. 3.1. Измерение горизонтального угла

 

Измерение вертикального угла. Пусть требуется измерить вертикальный угол, образованный линией AB (рис. 3.2). Но мы не можем установить вертикальный угломерный круг непосредственно в точке A. Чтобы обойти это небольшое затруднение, мы можем установить его в точке A ₁ на некоторой высоте i над точкой A, а над точкой B установить некоторую визирную цель такой же высоты, например веху. Тогда угол между линией A ₁ B ₁ и горизонтальной плоскостью будет равен вертикальному углу лини AB. Этот угол уже может быть измерен.

 

 

Рис. 3.2. Измерение вертикального угла

 

Сущность непосредственного измерения вертикального угла с помощью вертикального угломерного круга состоит в следующем.

1) Центр угломерного круга размещают в точке A ₁. (В принципе, это может быть любая точка на прямой AB.)

2) Плоскость вертикального угломерного круга совмещают с вертикальной плоскостью, проходящей через точки A и B.

3) Нулевой диаметр (диаметр, проходящий через нулевое деление лимба) вертикального круга приводят в горизонтальное положение.

4) Через центр вертикального угломерного круга и точку B ₁ проводят воображаемую прямую A ₁ В ₁. В пересечении линии A ₁ B ₁ со шкалой вертикального круга получим отсчет ν, который и будет значением вертикального угла.

Реальное измерение вертикального угла является более сложным. Эти сложности связаны с приведением нулевого диаметра в горизонтальное положение.

3.2. Геодезические приборы для измерения углов: теодолиты, их назначение и устройство (2Т30)

 

Рассмотрим геодезические приборы для измерения углов на примере теодолита 2Т30. Теодолит – прибор для измерения горизонтальных и вертикальных углов и расстояний с невысокой точностью. В зависимости от точности измерения углов теодолиты подразделяются на высокоточные, точные и технические. Погрешность однократного измерения угла (измерения одним приемом) высокоточным теодолитом составляет 0.5² - 1², точным 2² - 10², техническим - 15² - 30². В настоящее время выпускаются и используются в производстве только оптические теодолиты. Оптические теодолиты характеризуются наличием стеклянных угломерных кругов и оптической системы для передачи изображения делений на угломерных кругах в поле зрения микроскопа.

Основные части теодолита 2Т30 (и 2Т30П). Основание упаковочного футляра, становой винт, головка штатива. Подставка, подъемные винты. Горизонтальный угломерный круг состоит из двух соосно расположенных стеклянных кругов: нижнего, называемого лимбом, и верхнего, называемого алидадой. Лимб имеет закрепительный и наводящий винты; их наличие является признаком повторительного теодолита. Алидада с отсчетным устройством также имеет закрепительный и наводящий винты. Цилиндрический уровень с исправительными винтами. Колонки (подставки трубы). Зрительная труба, закрепительный и наводящий винты зрительной трубы. Ось вращения трубы. Визирная, или коллимационная, плоскость – вертикальная плоскость, проходящая через визирную ось. Объектив, окуляр, кремальера, диоптрийное кольцо. Защитный колпачок сетки нитей. Визир. Вертикальный угломерный круг также содержит лимб и алидаду. Микроскоп. Диоптрийное кольцо микроскопа.

Положение вертикального круга относительно зрительной трубы: если труба расположена окуляром к наблюдателю и вертикальный круг находится справа от зрительной трубы, то такое положение называется “Круг право” и обозначается КП или R; если вертикальный круг при этом расположен слева от зрительной трубы, то такое положение теодолита называют “Круг лево” и обозначают КЛ или L. Поворот трубы через зенит – вращение трубы в вертикальной плоскости на любой угол (до 360° и более). Если трубу перевести через зенит примерно на 180°, а затем повернуть вокруг вертикальной оси теодолита окуляром к наблюдателю, то положение КП изменится на КЛ и наоборот.

Схема прибора представлена на рис. 3.3, где оси теодолита обозначены следующим образом:

- ось вращения прибора, или главная ось прибора, WW – прямая, перпендикулярная плоскости алидады горизонтального круга и проходящая через ее центр;

- ось вращения зрительной трубы TT;

- визирная ось VV – воображаемая прямая, проходящая через оптический центр объектива и центр сетки нитей;

- ось цилиндрического уровня UU – касательная к внутренней поверхности ампулы уровня в нуль-пункте.

 

 

Рис. 3.3. Схема теодолита