Вырожденные кривые
Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты: § вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D > 0; § пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии D < 0; § вырожденная парабола — при условии D = 0: § пара вещественных параллельных прямых — при условии B < 0; § одна вещественная прямая (две слившиеся параллельные прямые) — при условии B = 0; § пара мнимых параллельных прямых (ни одной вещественной точки) — при условии B > 0.
14) Линейное, или векторное пространство 1. сложения, то есть каждой паре элементов множества 2. умножения на скаляр (то есть элемент поля P), то есть любому элементу
|

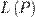 над полем P — это непустое множество L, на котором введены операции
над полем P — это непустое множество L, на котором введены операции ставится в соответствие элемент того же множества, обозначаемый
ставится в соответствие элемент того же множества, обозначаемый 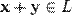 и
и и любому элементу
и любому элементу 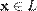 ставится в соответствие единственный элемент из
ставится в соответствие единственный элемент из  , обозначаемый
, обозначаемый 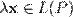 .
.


