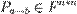Примеры. § В пространстве всех многочленов над полем один из базисов составляют степенные функции: .
§ Векторы § В пространстве всех многочленов над полем один из базисов составляют степенные функции: § Понятие базиса используется в бесконечномерном случае, например вещественные числа образуют линейное пространство над рациональными числами и оно имеет континуальный базис Гамеля и, соответственно, континуальную размерность. § РАЗМЕРНОСТЬ ВЕКТОРНОГО ПРОСТРАНСТВА [dimensionality of vector-space] — максимальное число линейно-независимых векторов в векторном (линейном) пространстве (см. Линейная зависимость векторов). Если это число конечно, то пространство называется конечномерным (многомерным). В противном случае — бесконечномерным. Пример конечномерного векторного пространства — множество возможных планов цеха из ст. “ Вектор ”. Размерность этого пространства равна 4. Точки на прямой действительных чисел образуют одномерное пространство.
17) Ма́трицей перехо́да от базиса Обозначается
|

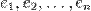 пространства
пространства  образуют базис тогда и только тогда, когда определитель матрицы, составленной из координатных столбцов этих векторов, не равен 0:
образуют базис тогда и только тогда, когда определитель матрицы, составленной из координатных столбцов этих векторов, не равен 0: 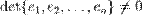 .
. .
. к базису
к базису  является матрица, столбцы которой — координаты разложения векторов
является матрица, столбцы которой — координаты разложения векторов 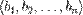 в базисе
в базисе