Однородные системы
Однородной системой линейных уравнений называется система вида: Нулевое решение Однородные системы всегда совместны, т.к. всегда существует тривиальное решение. Если существует любое ненулевое решение системы, то оно называется нетривиальным. Решения однородной системы обладают свойством линейности: Пусть дана однородная система (1), тогда набор векторов § § §
20) Лине́йный опера́тор — обобщение линейной числовой функции (точнее, функции y = kx) на случай более общего множества аргументов и значений. Линейные операторы, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин. Примеры линейных однородных операторов: § оператор дифференцирования: § оператор интегрирования: § оператор умножения на определённую функцию φ(t): y (t) = φ(t) x (t); § оператор интегрирования с заданным «весом» § оператор взятия значения функции f в конкретной точке x 0: L { f } = f (x 0)[4]; § оператор умножения вектора на матрицу: b = Ax; § оператор поворота вектора. Примеры линейных неоднородных операторов: § Любое аффинное преобразование; § § § y (t) = φ1(t) x (t) + φ2(t); где φ(t), φ1(t), φ2(t) — вполне определённые функции, а x (t) — преобразуемая оператором функция. 21) Характеристический многочлен матрицы — это многочлен, определяющий её собственные значения. Собственным вектором линейного преобразования A называется такой ненулевой вектор
Собственным значением линейного преобразования A называется такое число Упрощённо говоря, собственный вектор - любой ненулевой вектор x, который отображается оператором в коллинеарный λ x, а соответствующий скаляр λ называется собственным значением оператора. 22) Теоре́ма Га́мильтона — Кэ́ли — известная теорема из теории матриц, названная в честь Уильяма Гамильтона и Артура Кэли. Непосредственная проверка оправдывает это утверждение для матрицы порядка 2: Характеристический многочлен
тогда c (A) = A 2 − (a 11 + a 22) A + (a 11 a 22 − a 12 a 21) E =
§ Теорема Гамильтона — Кэли обуславливает существование аннулирующего многочлена. § Теорема Гамильтона — Кэли эквивалентна утверждению, что характеристический многочлен делится без остатка на минимальный многочлен. 23) ЛИНЕЙНАЯ МОДЕЛЬ ОБМЕНА В качестве примера математической модели экономического процесса, приводящей к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли). Пусть имеется n стран S1, S2,..., Sn, национальный доход каждой из которых равен соответственно x1, x2,..., xn. Обозначимкоэффициентами aij долю национального дохода, которую страна Sj тратит на покупку товаров у страны Si. Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е. a1j + a2j +... + anj = 1 (j = 1,2,...,n). Рассмотрим матрицу
которая получила название структурной матрицы торговли. В соответствии с предыдущим равенством сумма элементов любого столбца матрицы А равна 1. Для любой страны Si (i = 1,2,...,n) выручка от внутренней и внешней торговли составит: pi = ai1 x1 + ai2 x2 +... + ain xn. Для сбалансированной торговли необходима бездефицитность торговли каждой страны Si, т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода: pi > = xi (i = 1,2,...,n). 24) Скалярным произведением в векторном пространстве 1. для любых трех элементов 2. для любых 3. для любого Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.
|

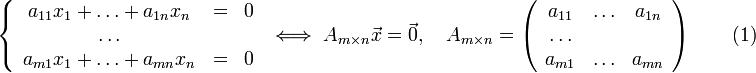
 системы (1) называется тривиальным решением.
системы (1) называется тривиальным решением. размера
размера  называется фундаментальной системой решений (ФСР) (1), если:
называется фундаментальной системой решений (ФСР) (1), если: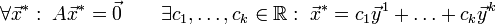
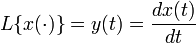 ;
;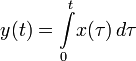 ;
;
 ;
; ;
;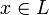 , что для некоторого
, что для некоторого 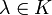
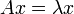


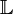 над полем
над полем  называется функция
называется функция  для элементов
для элементов  , принимающая значения в
, принимающая значения в 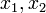 и
и 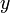 пространства
пространства  справедливо равенство
справедливо равенство 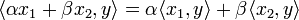 (линейность скалярного произведения по первому аргументу);
(линейность скалярного произведения по первому аргументу); и
и 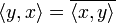 , где черта означает комплексное сопряжение (эрмитова симметричность);
, где черта означает комплексное сопряжение (эрмитова симметричность);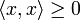 , причем
, причем  только при
только при 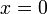 (положительная определенность скалярного произведения).
(положительная определенность скалярного произведения). действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.
действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.


