Примеры. § В трёхмерном вещественном векторном пространстве векторов введение скалярного произведения по формуле превращает это пространство в евклидово
§ В трёхмерном вещественном векторном пространстве векторов § В любом евклидовом пространстве (размерности n) всегда можно выбрать[1] ортонормированный базис при разложении векторов по которому:
скалярное произведение будет выражаться приведенной выше формулой:
25) Рассмотрим свойства скалярного произведения. 1. Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов Очевидно, из определения скалярного произведения:
2. Для любого числа λ и любых векторов
Для любых векторов 1. Для любого вектора Действительно, так как Из этого свойства в частности следует 2. Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны. 26) Ортонормированная система Для любых элементов этой системы φ i,φ j скалярное произведение (φ i,φ j) = δ ij, где δ ij — символ Кронекера. Ортонормированная система в случае её полноты может быть использована в качестве базиса пространства. При этом разложение любого элемента Ортогонализация ― алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства V ортогональной системы ненулевых векторов, порождающих то же самое подпространство в V. Наиболее известным является процесс Грама ― Шмидта, при котором по линейно независимой системе 27) Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора. Пусть Функция
где Матрицу
|

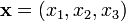 введение скалярного произведения по формуле
введение скалярного произведения по формуле 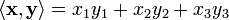 превращает это пространство в евклидово пространство. Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства).
превращает это пространство в евклидово пространство. Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства).
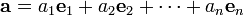 ,
, итд,
итд,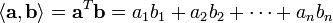 .
.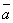 и
и 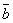
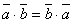 .
. .
. имеем:
имеем: .
. выполняется равенство
выполняется равенство 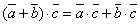 .
.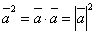 .
.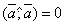 , то
, то 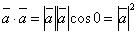 .
.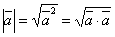 .
.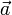 может быть вычислено по формулам:
может быть вычислено по формулам: 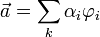 , где
, где 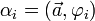 .
.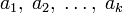 строится ортогональная система
строится ортогональная система 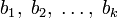 такая, что каждый вектор bi линейно выражается через
такая, что каждый вектор bi линейно выражается через 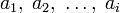 , то есть матрица перехода от { ai } к { bi } ― верхнетреугольная матрица.
, то есть матрица перехода от { ai } к { bi } ― верхнетреугольная матрица. есть векторное пространство над полем
есть векторное пространство над полем  и
и  — базис в
— базис в 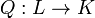 называется квадратичной формой, если её можно представить в виде
называется квадратичной формой, если её можно представить в виде
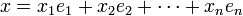 , а
, а  — некоторые элементы поля
— некоторые элементы поля  называют матрицей квадратичной формы в данном базисе. В случае, если характеристика поля
называют матрицей квадратичной формы в данном базисе. В случае, если характеристика поля 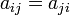 .
.


