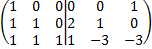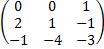Найти матрицу линейного преобразования
Найти матрицу линейного оператора φ в базисе e1=(1, 1, 1), e2=(0, 1, 1), e3=(0, 0, 1), если φ(x1,x2,x3)=(–x2+x3, x1+x2, 4x1–3x3). Решение Находим φ(e1)=(–1+1, 1+1, 4*1–3*1)=(0,2,1) φ(e2)=(–1+1, 0+1, 4*0–3*1)=(0,1,-3) φ(e3)=(–0+1, 0+0, 4*0–3*1)=(1,0,-3)
Рассмотрим матрицу из векторов e1=(1, 1, 1), e2=(0, 1, 1), e3=(0, 0, 1):
С помощью элементарных преобразований строк приводим матрицу с лева к единичной, тогда матрица справа это матрица линейного оператора.
Ответ
|
.
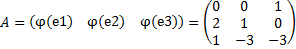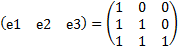. Так как матрица не единичная, то матицу A нужно привести в стандартный базис.
