Использовании ОМНК для корректировки гетероскедастичности.
· предполагаем, что среднее значение остаточных величин равно нулю; · дисперсия пропорциональна величине
где
· предполагается, что
Уравнение при модель примет вид:
· можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе · дисперсия остатков будет теперь величиной постоянной, т. е. · от регрессии
Уравнение регрессии примет вид:
а исходные данные для данного уравнения будут иметь вид:
· переменные ·
Соответственно получим следующую систему нормальных уравнений:
Если преобразованные переменные При МНК для переменных в отклонениях от средних уровней коэффициент регрессии При использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии
Тест Голдфелда Кванта (Goldfeld-Quandt) В тесте предполагается, что дисперсия остатков зависит от какого-либо регрессора.
Схема проведения теста: 1. Упорядочить выборку в соответствии с ростом 2. Наблюдения делят на две группы: соответствующие большим и малым значениям Х (наблюдения, соответствующие средним значениям, могут быть опущены 3. Оценить модели для первых Рассчитать статистику,которая имеет распределение Фишера с
4. Проверить наличие гетегоскедастичности Если
|

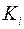 , т.е.
, т.е.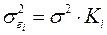 ,
,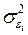 – дисперсия ошибки при конкретном
– дисперсия ошибки при конкретном 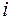 -м значении фактора;
-м значении фактора;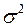 – постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
– постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;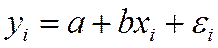
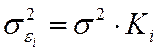
 .
.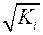 ;
;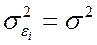
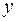 по
по  мы перейдем к регрессии на новых переменных:
мы перейдем к регрессии на новых переменных: 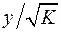 и
и 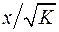 .
.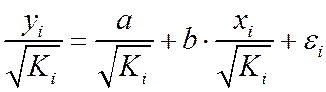 ,
,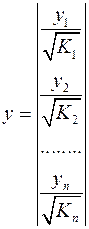 ,
, 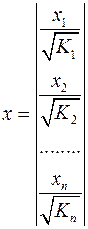 .
.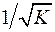 .
.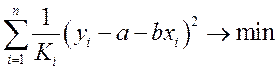 .
.
 .
.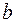 определяется по формуле:
определяется по формуле: 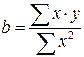 .
.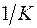 .
.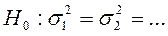
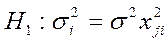
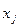
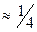 наблюдений); число наблюдений в каждой группе
наблюдений); число наблюдений в каждой группе 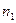 и
и 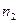 ).
).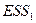 и
и 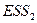 .
.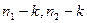 степенями свободы в случае истинности нулевой гипотезы,
степенями свободы в случае истинности нулевой гипотезы,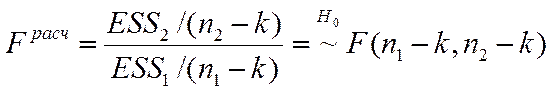
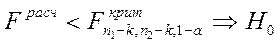 не отвергаем,
не отвергаем,


